This is a problem that brings me memories of a time when I had a folding bike and lived in a place where there is excellent public transportation.

Jill Rides Again is problem 507 in the UVa Online Judge. Even though I include the problem description in this post, I encourage you to visit the UVa Online Judge because there you will be able to submit your solution to get it judged.

Problem

Jill likes to ride her bicycle, but since the pretty city of Greenhills where she lives has grown, Jill often uses the excellent public bus system for part of her journey. She has a folding bicycle which she carries with her when she uses the bus for the first part of her trip. When the bus reaches some pleasant part of the city, Jill gets off and rides her bicycle. She follows the bus route until she reaches her destination or she comes to a part of the city she does not like. In the latter event she will board the bus to finish her trip.

Through years of experience, Jill has rated each road on an integer scale of “niceness.” Positive niceness values indicate roads Jill likes; negative values are used for roads she does not like. There are not zero values. Jill plans where to leave the bus and start bicycling, as well as where to stop bicycling and re-join the bus, so that the sum of niceness values of the roads she bicycles on is maximized. This means that she will sometimes cycle along a road she does not like, provided that it joins up two other parts of her journey involving roads she likes enough to compensate. It may be that no part of the route is suitable for cycling so that Jill takes the bus for its entire route. Conversely, it may be that the whole rute is so nice Jill will not use the bus at all.

Since there are many different bus routes, each with several stops at which Jill could leave or enter the bus, she feels that a computer program could help her identify the best part to cycle for each bus route.

Input

The input file contains information on several bus routes. The first line of the file is a single integer b representing the number of route descriptions in the file. The identifier for each route (r) is the sequence number within the data file, 1 <= r <= b. Each route description begins with the number of stops on the route: an integer s, 2 <= s <= 20,000 on a line by itself. The number of stops is followed by s - 1 lines, each line i (1 <= i < s) is an integer n_i, representing Jill’s assessment of the niceness of the road between the two stops i and i + 1.

Output

For each route r in the input file, your program should identify the beginning bus stop i and the ending bus stop j that correspond to the segment of the route which yields the maximal sum of niceness, m = n_i + n_i+1 + ... + n_j-1. If more than one segment is maximally nice, choose the one with the longest cycle ride (largest j - i). To break ties in longest maximal segments, choose the segment that begins with the earliest stop (lowest i). For each route r in the input file, print a line in the form:

The nicest part of route r is between stops i and j

However, if the maximal sum is not positive, your program should print:

Route r has no nice parts

Sample Input

Sample Output

The nicest part of route 1 is between stops 2 and 3
The nicest part of route 2 is between stops 3 and 9
Route 3 has no nice parts

Analysis

Jill Rides Again is similar to the Maximum Subarray Problem [Bentley84]. For that reason, we analyze the Maximum Subarray Problem and derive a solution to Jill Rides Again.

For a given sequence of integers, the Maximum Subarray Problem consists in finding the maximum sum that is positive amongst the sums of subsequences. When there is no positive number in the sequence, the maximum sum is zero and corresponds to the empty subsequence. For example, consider the following sequence. The maximum sum for the sequence is positive and is 11. The maximum sum corresponds to subsequences A and B.

 -1   6  -6   2  -4   5   6  -6   6
                     -------
                        A
                     ---------------
                            B

A straightforward solution consists of computing the sum for each subsequence and selecting the maximum sum. Consider the following C implementation.

#include <stdio.h>

int main() {
  int b, r = 0, s, i, j, curr_sum, max_sum, n;
  int road[20000];
  scanf("%d", &b);
  while(r++ < b) {
    scanf("%d", &s);
    for(i = 0; i < s - 1; i++) {
      scanf("%d", &n);
      road[i] = n;
    }
    for(max_sum = i = 0; i < s - 1; i++) {        // START
      for(curr_sum = 0, j = i; j < s - 1; j++) {  // END
        curr_sum += road[j];
        if(curr_sum > max_sum) {
          max_sum = curr_sum;
        }
      }
    }
    if(max_sum == 0) {
      printf("Route %d has no nice parts\n", r);
    } else {
      printf("The nicest part of route %d has niceness %d\n", r, max_sum);
    }
  }
  return 0;
}

Listing 1: Solution that computes the sum of each subsequence and selects the maximum

The solution computes the sum for each subsequence in the following way. The solution visits each start position with every iteration of loop START. For a given start position, the solution computes the sum of each subsequence that starts there by means of loop END. For example, when the start position is the first position (i = 0), the solution computes the sum of the following subsequences.

          -1   6  -6   2  -4   5   6  -6   6
[0, 0]   ----
[0, 1]   --------
[0, 2]   ------------
[0, 3]   ----------------
[0, 4]   --------------------
[0, 5]   ------------------------
[0, 6]   ----------------------------
[0, 7]   --------------------------------
[0, 8]   ------------------------------------

The solution selects the maximum sum max_sum after computing the sum for each subsequence. The following graph illustrates how the solution selects the maximum sum for each subsequence that starts in the first position. For subsequence [0, 0], the sum is negative and thus ignored. For subsequence [0, 1], the sum is 5 and the maximum sum so far, thus the sum is recorded as the current maximum. For subsequences that end in positions 2, 3, 4, and 5, each sum is not bigger than 5 and thus ignored. The sum of subsequence [0, 6] is 8 and becomes the maximum. The remaining two subsequences are ignored.

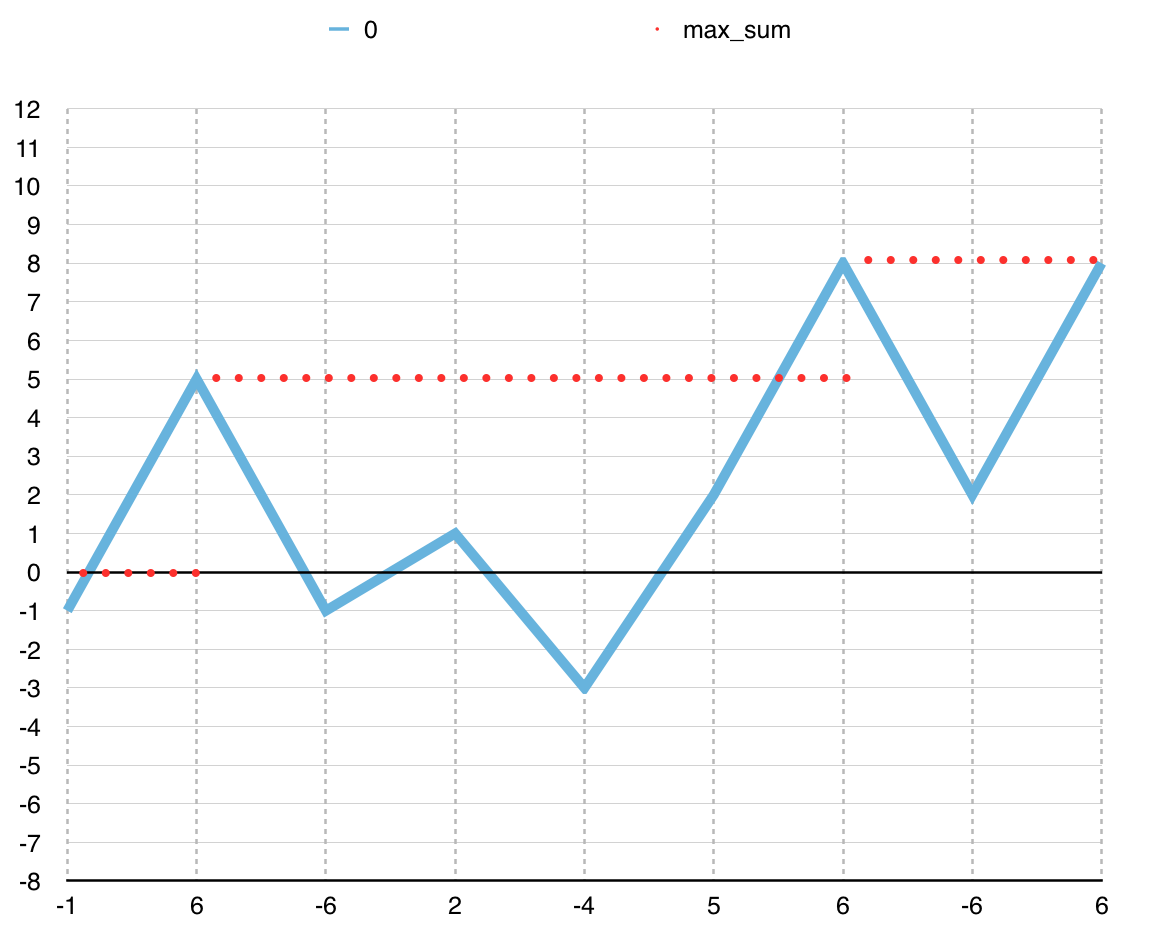
Figure 2: State of program in Listing 1 for the subsequences that start in the first position. The line in blue indicates the value of curr_sum for each end position. The dotted red line indicates the value of max_sum for each end position.

The problem with the straightforward solution is that it is too slow. For the given sequence, the solution considers the 45 subsequences illustrated in the following graph and computes the sum for each. For a sequence of n elements, there are 1/2(n^2 + n) subsequences. For the maximum sequence length considered by the problem statement of Jill Rides Again (i.e. 20,000), the solution considers 100,010,000 subsequences and thus timeouts in the UVa Online Judge.

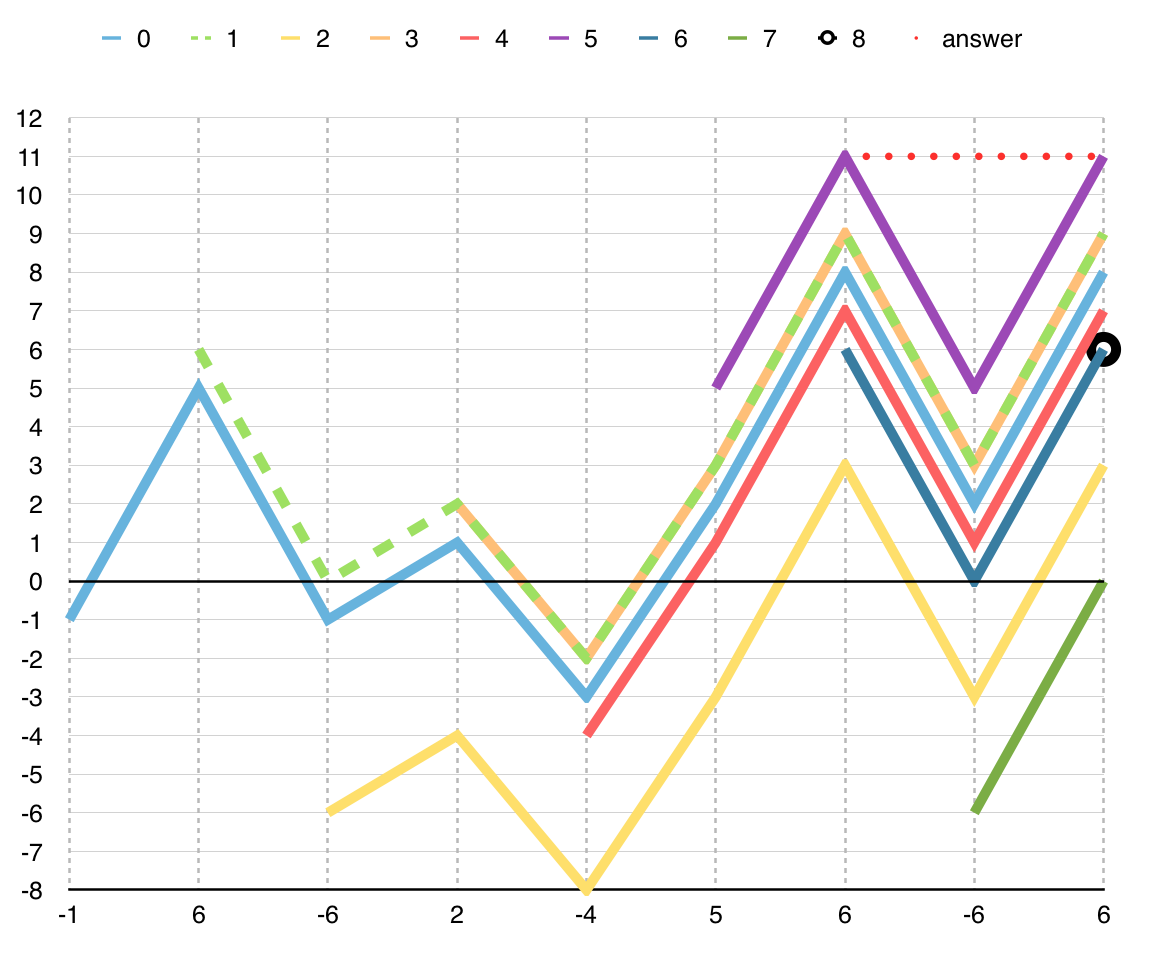
Figure 3: State of program in Listing 1 for all subsequences. Each line corresponds to a start position. For each line, each data point indicates the value of curr_sum for the subsequence that ends in the corresponding position. Line answer indicates the last time max_sum is updated.

The fastest solution to the Maximum Subarray Problem is Kadane’s Algorithm [Bentley84]. Consider the following C implementation.

#include <stdio.h>

int main() {
  int b, r = 0, s, i, max_here, max_sum, n;
  scanf("%d", &b);
  while(r++ < b) {
    scanf("%d", &s);
    for(max_sum = max_here = i = 0; i < s - 1; i++) { // BEFORE
      scanf("%d", &n);
      max_here += n; //................................. SUM
      if(max_here < 0) {
        max_here = 0; //................................ RESET
      }
      if(max_here > max_sum) {
        max_sum = max_here; //.......................... UPDATE
      }
    }
    if(max_sum == 0) {
      printf("Route %d has no nice parts\n", r);
    } else {
      printf("The nicest part of route %d has niceness %d\n", r, max_sum);
    }
  }
  return 0;
}

Listing 4: Our implementation of Kadane’s Algorithm

Kadane’s Algorithm is the fastest solution because Kadane’s Algorithm considers n subsequences for a sequence of n elements. For example, for the given sequence, Kadane’s Algorithm considers only 9 subsequences instead of the 45 that the solution in Listing 1 considers. The following graph indicates the 9 subsequences. For each position of the sequence, Kadane’s Algorithm considers only one subsequence. That subsequence is the longest subsequence that ends in the position and has the maximum sum (i.e. max_here).

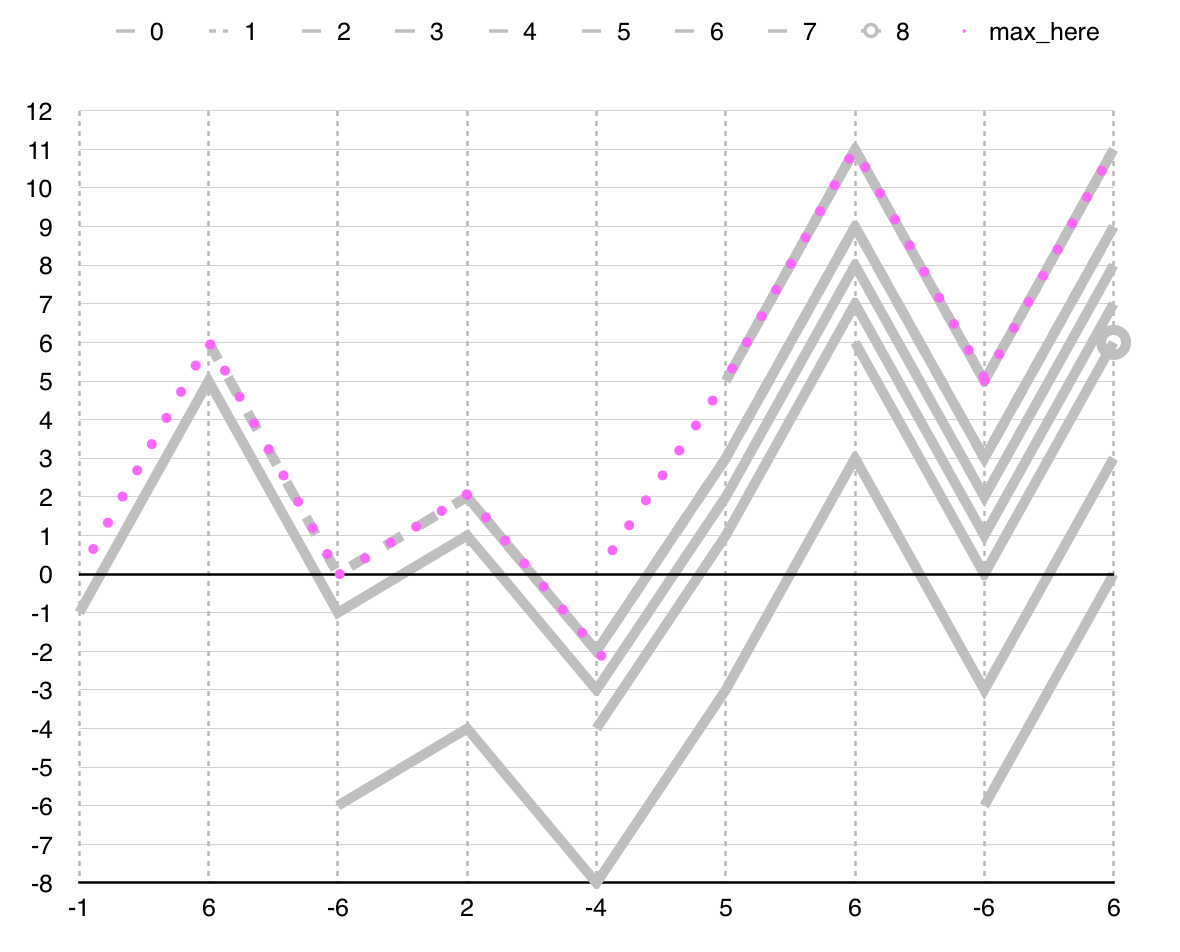
Figure 5: The 9 subsequences considered by Kadane’s Algorithm. The dotted line in pink indicates the 9 subsequences. Consider any position in the sequence. When the dotted line is not over a gray line, the current sequence is the empty sequence. That is the case for positions 0 (element -1) and 5 (element -4). When the dotted pink line is over a gray line, the prefix of the gray line is the subsequence for that position. That subsequence is the longest subsequence that ends in the position.

As Kadane’s Algorithm iterates over positions, it preserves the invariant condition that max_sum is the maximum sum so far. The maximum sum so far corresponds to a subsequence that either ends at a previous position (and thus line UPDATE is not executed) or ends in the current position (and thus line UPDATE is executed). Consider the execution of Kadane’s Algorithm for the given sequence. Before visiting the first position, there is no maximum sum (i.e. max_sum is zero at line BEFORE). For each position, line SUM assigns to max_here the sum of the subsequence that ends here and has the maximum sum. For the first position, SUM assigns -1 to max_here. When the subsequence that ends here and has the maximum sum is negative, line RESET discards the sum so that when we visit a positive position, line SUM computes the maximum sum there. For the first position, RESET resets max_here because the subsequence [0, 0] has sum -1. Preserving -1 and then visiting the second position would correspond to moving over the line labeled 0 in Figure 6. What we want is to move over the line labeled 1 when we visit the second position. When the sum of the subsequence that ends here and has the maximum sum is greater than the current maximum sum, line UPDATE updates the maximum sum so far max_sum and thus preserves the invariant condition. For the first position, there is no update. For the second position, there is an update and that corresponds to the star to the left in Figure 6.

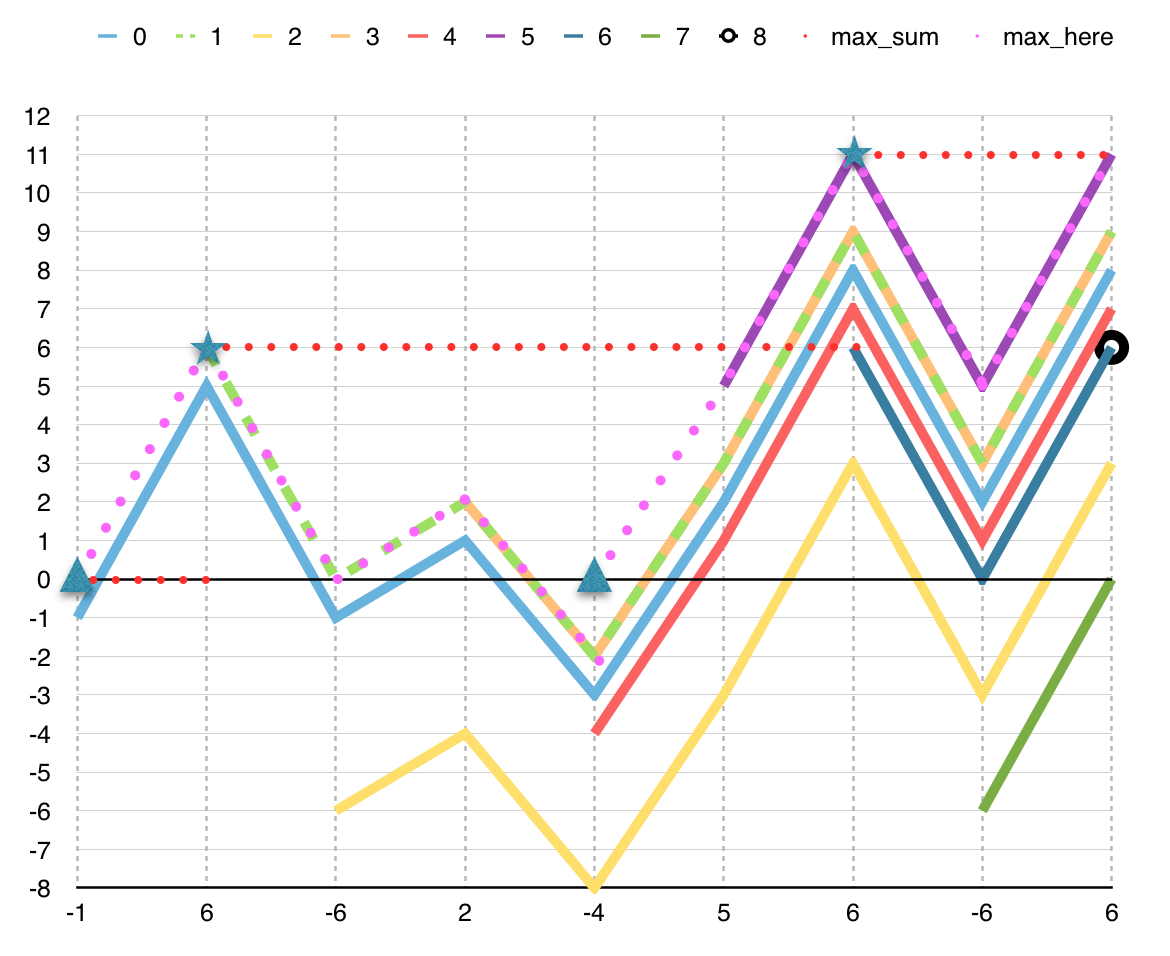
Figure 6: State of Kadane’s Algorithm in Listing 4 laid over the state of solution in Listing 1. Triangles indicate reset of max_here. Stars indicate update of max_sum. For each position, the line max_here indicates the sum of the subsequence that ends in the position and has the maximum sum.

Solution

Consider our solution to Jill Rides Again below. Our solution to Jill Rides Again is our implementation of Kadane’s Algorithm in Listing 2 with changes in the labeled lines.

#include <stdio.h>

int main() {
  int b, r = 0, s, i, max_here, max_sum, n;
  int max_i, max_j, i_here; //....................................... A
  scanf("%d", &b);
  while(r++ < b) {
    scanf("%d", &s);
    max_j = max_i = i_here = 0; //................................... B
    for(max_sum = max_here = i = 0; i < s - 1; i++) {
      scanf("%d", &n);
      max_here += n;
      if(max_here < 0) {
        max_here = 0;
        i_here = i + 1; //........................................... C
      }
      if(max_here > max_sum
         || (max_here == max_sum && i - i_here > max_j - max_i)) { // D
        max_sum = max_here;
        max_i = i_here; //........................................... E
        max_j = i; //................................................ F
      }
    }
    if(max_sum == 0) {
      printf("Route %d has no nice parts\n", r);
    } else {
      printf("The nicest part of route %d is between stops %d and %d\n", r, max_i+1, max_j+2); // G
    }
  }
  return 0;
}

Listing 7: Our solution to Jill Rides Again

The following figure illustrates the execution of our solution to Jill Rides Again on the given sequence. For a given position, our changes track the boundaries of the subsequence that ends here and the maximum so far. When Kadane’s Algorithm resets max_here, that corresponds to discarding the subsequence that ends here and thus line C resets the left boundary i_here of the subsequence. When Kadane’s Algorithm updates the maximum so far, lines E and F update its boundaries max_i and max_j with the boundaries of the subsequence that ends here. The second disjunct in line D corresponds to the requirement that we return the longest maximal subsequence. When that disjunct is satisfied, our solution pushes the right boundary of the maximum sum so far but not its value. That is what happens in the rightmost star in Figure 8.

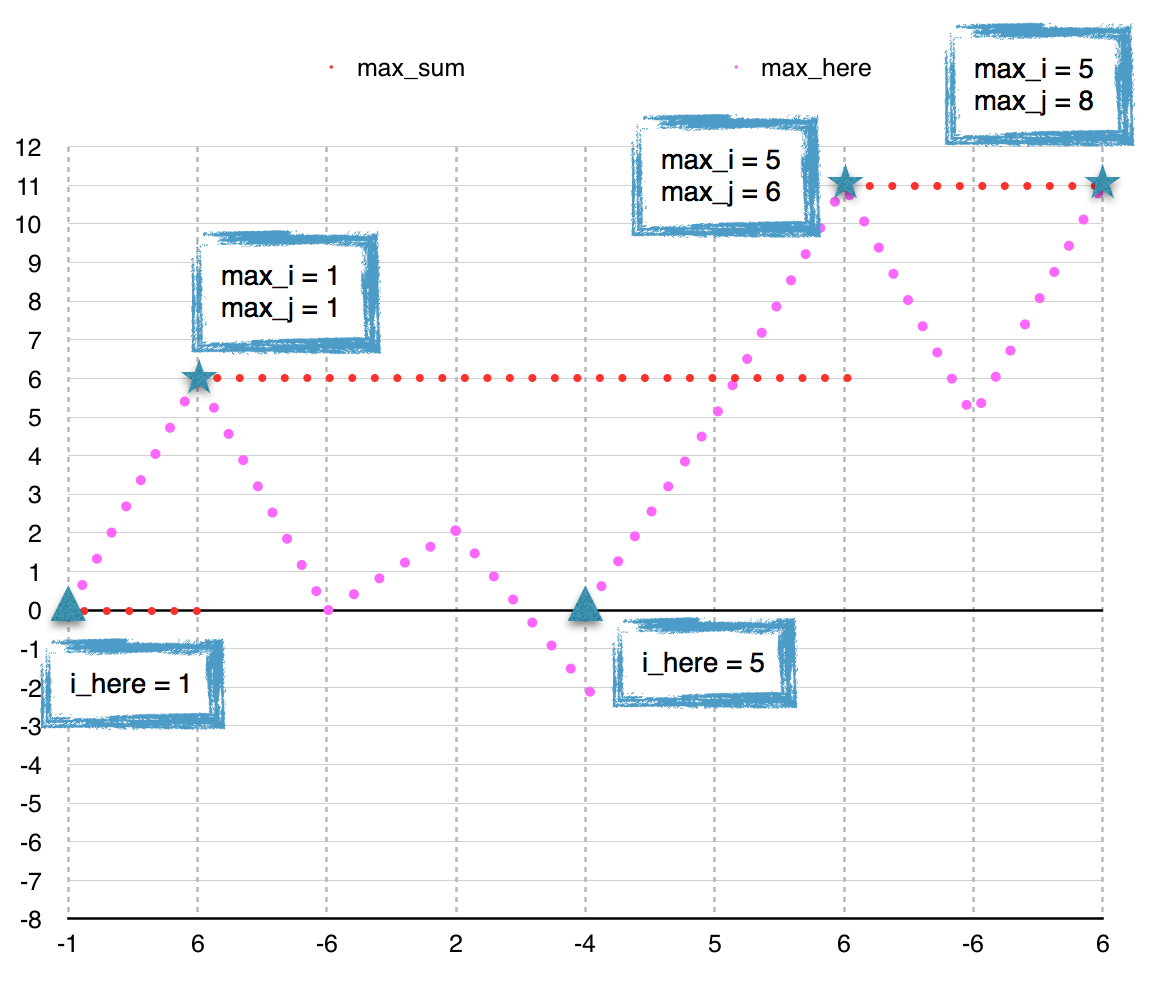
Figure 8: Execution of our solution to Jill Rides Again in Listing 7. Triangles indicate reset of the beginning of the subsequence that ends at each subsequent position, i_here. Stars indicate update of the boundaries of the maximum subsequence so far, max_i and max_j.

Our solution was accepted by UVa Online Judge.

Summary

Jill Rides Again is a variant of the classical Maximum Subarray Problem [Bentley84]. The solution to the Maximum Subarray Problem is Kadane’s Algorithm. Kadane’s Algorithm is a model solution for problems that require computing maximum subsequences. Thus, we based our solution to Jill Rides Again on Kadane’s Algorithm.

What was your experience solving this problem? Let me know in the comments.

References

[Bentley84] Bentley, Jon (1984), “Programming pearls: algorithm design techniques”, Communications of the ACM 27 (9): 865–871, doi:10.1145/358234.381162.