An interview question in the wild, the Category Problem asks to model a graph of categories of goods in SQL. The sample solution involves a couple of recursive SQL queries that traverse the edges of the model graph. The sample solution works in PostgreSQL 9.6. This post includes a reference implementation in Ruby.

Problem

The problem asks you to implement in SQL the following rules.

There are products. Each product has a name.
There are categories. Each category has a name.
Each product may belong to one or more categories.
Each category may have subcategories.
Categories that have products do not have subcategories.
Each category has at most one parent.
You may ask a product for its corresponding categories.
You may ask a category for its corresponding products.

Consider the following diagram of an example state consisting of products and categories.

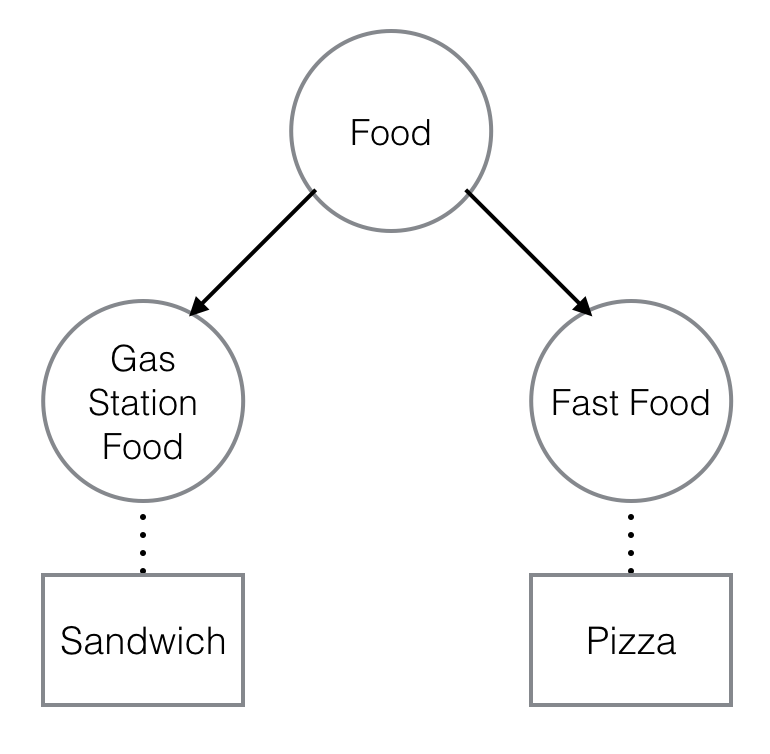
Example

In the diagram, a box corresponds to a product and a circle to a category. Arrows start from a parent category and end in a child category. This is relation subcategory. Dotted lines connect categories with their corresponding products. This is relation belongs-to.

Your database must forbid violations of the rules. Consider the following examples. By rule 5, it must not be possible to add products to category Food. By rule 6, it must not be possible for Fast Food to be subcategory of Food and Home Delivered Goods.

The categories of Sandwich are Gas Station Food and Food. The categories of Pizza are Fast Food and Food.

The only product of category Fast Food is Pizza. The products of category Food are Sandwich and Pizza.

Solution

The sample solution is the following.

-- PART I: Database Schema

CREATE TABLE products (
  id serial PRIMARY KEY,
  name varchar(50)
);

CREATE TABLE categories (
  id serial PRIMARY KEY,
  name varchar(50),
  parent integer REFERENCES categories(id)
);

CREATE TABLE p_c (
  pid integer REFERENCES products(id),
  cid integer REFERENCES categories(id)
);

CREATE FUNCTION if_no_sub_c(cid integer)
  RETURNS bool AS
  $func$
    SELECT NOT EXISTS (SELECT 1 FROM categories WHERE parent = cid);
  $func$ LANGUAGE sql STABLE;

ALTER TABLE p_c ADD CONSTRAINT if_no_sub_c_check
  CHECK (if_no_sub_c(cid));

CREATE FUNCTION if_no_prod(id integer)
  RETURNS bool AS
  $func$
    SELECT NOT EXISTS (SELECT 1 FROM p_c WHERE cid = id);
  $func$ LANGUAGE sql STABLE;

ALTER TABLE categories ADD CONSTRAINT if_no_prod_check
  CHECK (if_no_prod(parent));

-- PART II: Recursive queries

CREATE FUNCTION categories(product_id integer)
  RETURNS TABLE (category varchar(50)) AS
  $func$
    WITH RECURSIVE cats(pid, cid, name, parent) AS (
      SELECT pid, categories.*
      FROM p_c, categories
      WHERE cid = id
    UNION ALL
      SELECT pid, categories.*
      FROM cats, categories
      WHERE cats.parent = categories.id
    )
    SELECT name FROM cats WHERE pid = product_id;
  $func$ LANGUAGE sql;

CREATE FUNCTION products(category_id integer)
  RETURNS TABLE (products varchar(50)) AS
  $func$
    WITH RECURSIVE prods(cid, parent, pid, product) AS (
        SELECT cid, parent, pid, products.name
        FROM p_c, products, categories
        WHERE pid = products.id AND cid = categories.id
      UNION ALL
        SELECT par.id, par.parent, pid, product
        FROM prods, categories AS par
        WHERE prods.parent = par.id
    )
    SELECT product FROM prods WHERE cid = category_id
  $func$ LANGUAGE sql;

The sample solution consists of two parts. The first part is the construction of the database schema required by rules 1 to 6. The second part is the construction of two recursive queries, one for rule 7 and one for rule 8. Section Reference implementation in Ruby includes a reference implementation in Ruby that you can use to understand the semantics of the sample solution.

Database schema

The following is an explanation of the construction of the database schema.

1. Each product has a name.

We create a table of products.

CREATE TABLE products (
  id serial PRIMARY KEY,
  name varchar(50)
);

Example usage.

INSERT INTO products (name) VALUES ('sandwich');
SELECT * FROM products;

Gives.

INSERT 0 1
 id |   name   
----+----------
  1 | sandwich
(1 row)

2. Each category has a name.

We create a table of categories.

CREATE TABLE categories (
  id serial PRIMARY KEY,
  name varchar(50)
);

Example usage.

INSERT INTO categories (name) VALUES ('gas station food');
SELECT * FROM categories;

Gives.

INSERT 0 1
 id |       name       
----+------------------
  1 | gas station food
(1 row)

3. Each product may belong to one or more categories.

Meaning, each product may or may not belong to one or more categories. We assume that categories may correspond to multiple products. Given these reasons, relation belongs-to is a many-to-many relation. The following associative table (a.k.a. cross-reference table) corresponds to relation belongs-to.

CREATE TABLE belongs_to (
  pid integer REFERENCES products(id),
  cid integer REFERENCES categories(id)
);

Example usage.

INSERT INTO belongs_to (pid, cid) VALUES (1, 1);
SELECT products.name AS product, categories.name AS category
  FROM products, belongs_to, categories
  WHERE products.id = pid AND cid = categories.id;

Gives.

INSERT 0 1
 product  |     category     
----------+------------------
 sandwich | gas station food
(1 row)

4. Each category may have subcategories.
AND
6. Each category has at most one parent.

We address rules 4 and 6 in one step. These rules mean that relation subcategory is a one-to-many relation. We implement relation subcategory by appending an additional attribute to table categories.

ALTER TABLE categories
  ADD COLUMN parent integer
  REFERENCES categories(id);

Example usage.

INSERT INTO categories (name) VALUES ('food');
UPDATE categories SET parent = 2 WHERE id = 1;
SELECT c1.name AS parent, c2.name AS child
  FROM categories AS c1, categories AS c2
  WHERE c1.id = c2.parent;

Gives.

INSERT 0 1
UPDATE 1
 parent |      child       
--------+------------------
 food   | gas station food
(1 row)

5. Categories that have products do not have subcategories.

We implement this rule by functions if_no_sub_c and if_no_prod.

We constraint relation belongs-to by function if_no_sub_c.

CREATE FUNCTION if_no_sub_c(cid integer)
  RETURNS bool AS
  $func$
    SELECT NOT EXISTS (SELECT 1 FROM categories WHERE parent = cid);
  $func$ LANGUAGE sql STABLE;

ALTER TABLE p_c ADD CONSTRAINT if_no_sub_c_check
  CHECK (if_no_sub_c(cid));

Example usage.

INSERT INTO products (name) VALUES ('pizza');
SELECT products.name AS product, categories.name AS category
  FROM products, p_c, categories
  WHERE products.id = pid AND cid = categories.id;
INSERT INTO p_c (pid, cid)
  SELECT products.id, categories.id
  FROM products, categories
  WHERE products.name = 'pizza' AND categories.name = 'food';
SELECT products.name AS product, categories.name AS category
  FROM products, p_c, categories
  WHERE products.id = pid AND cid = categories.id;

Gives.

INSERT 0 1
 product  |     category
----------+------------------
 sandwich | gas station food
(1 row)

ERROR:  new row for relation "p_c" violates check constraint "if_no_sub_c_check"
DETAIL:  Failing row contains (2, 2).
 product  |     category
----------+------------------
 sandwich | gas station food
(1 row)

We constraint relation subcategory by function if_no_prod.

CREATE FUNCTION if_no_prod(id integer)
  RETURNS bool AS
  $func$
    SELECT NOT EXISTS (SELECT 1 FROM p_c WHERE cid = id);
  $func$ LANGUAGE sql STABLE;

ALTER TABLE categories ADD CONSTRAINT if_no_prod_check
  CHECK (if_no_prod(parent));

Example usage.

SELECT * FROM categories;
INSERT INTO categories (name, parent)
  SELECT 'fast food', gsf.id
  FROM categories AS gsf
  WHERE gsf.name = 'gas station food';
SELECT * FROM categories;

Gives.

 id |       name       | parent
 ----+------------------+--------
   2 | food             |
   1 | gas station food |      2
(2 rows)

ERROR:  new row for relation "categories" violates check constraint "if_no_prod_check"
DETAIL:  Failing row contains (3, fast food, 1).
 id |       name       | parent
 ----+------------------+--------
   2 | food             |
   1 | gas station food |      2
(2 rows)

Recursive queries

The following is an explanation of the two recursive queries.

7. You may ask a product for its corresponding categories.

This rule asks for those categories that are ancestors of a given product in relation subcategory. We compute the ancestor categories by function categories.

CREATE FUNCTION categories(product_id integer)
  RETURNS TABLE (category varchar(50)) AS
  $func$
    WITH RECURSIVE cats(pid, cid, name, parent) AS (
      SELECT pid, categories.*
      FROM p_c, categories
      WHERE cid = id
    UNION ALL
      SELECT pid, categories.*
      FROM cats, categories
      WHERE cats.parent = categories.id
    )
    SELECT name FROM cats WHERE pid = product_id;
  $func$ LANGUAGE sql;

For a given product, the computation starts from the categories that contain the product. Those categories are given by the following SELECT statement.

...
    WITH RECURSIVE cats(pid, cid, name, parent) AS (
      SELECT pid, categories.*
      FROM p_c, categories
      WHERE cid = id
    UNION ALL
...

The SELECT statement is the base case of a recursive WITH clause. The recursive step consists in selecting those categories that are parent of some category given by a previous recursive call. The the recursive step corresponds to the following SELECT statement.

...
    UNION ALL
      SELECT pid, categories.*
      FROM cats, categories
      WHERE cats.parent = categories.id
    )
...

The result of the recursive WITH clause is projected onto the name before returning by the following SELECT statement.

...
    )
    SELECT name FROM cats WHERE pid = product_id;
  $func$ LANGUAGE sql;
...

Example usage.

SELECT categories(id) FROM products WHERE name = 'sandwich';
SELECT categories(id) FROM products WHERE name = 'pizza';
INSERT INTO categories (name, parent)
  SELECT 'fast food', categories.id
  FROM categories
  WHERE name = 'food';
INSERT INTO p_c (pid, cid)
  SELECT products.id, categories.id
  FROM products, categories
  WHERE products.name = 'pizza' AND categories.name = 'fast food';
SELECT categories(id) FROM products WHERE name = 'pizza';

Gives.

    categories
------------------
  gas station food
  food
(2 rows)

 categories
------------
 (0 rows)

INSERT 0 1
INSERT 0 1
 categories
------------
 fast food
 food
(2 rows)

8. You may ask a category for its corresponding products.

This rule asks that we collect the products of categories that are descendant of given category in relation subcategory. The following function products implements the rule.

CREATE FUNCTION products(category_id integer)
  RETURNS TABLE (products varchar(50)) AS
  $func$
    WITH RECURSIVE prods(cid, parent, pid, product) AS (
        SELECT cid, parent, pid, products.name
        FROM p_c, products, categories
        WHERE pid = products.id AND cid = categories.id
      UNION ALL
        SELECT par.id, par.parent, pid, product
        FROM prods, categories AS par
        WHERE prods.parent = par.id
    )
    SELECT product FROM prods WHERE cid = category_id
  $func$ LANGUAGE sql;

Example usage.

SELECT products(id) FROM categories WHERE name = 'food';
SELECT products(id) FROM categories WHERE name = 'fast food';
SELECT products(id) FROM categories WHERE name = 'gas station food';

Gives.

 products
----------
 sandwich
 pizza
(2 rows)

products
----------
 pizza
(1 row)

products
----------
 sandwich
(1 row)

Reference implementation in Ruby

The reference implementation is the following.

class Product

  attr_reader :name
  attr_accessor :parent_categories

  def initialize name
    @name = name
    @parent_categories = []
  end

  def to_s
    @name
  end

  alias inspect to_s

  def categories
    @parent_categories.reduce [] do |acc, c|
      begin
        acc << c
        c = c.parent
      end while c
      acc
    end
  end

end

class Category

  attr_reader :name, :products, :children
  attr_accessor :parent

  def initialize name
    @name = name
    @products = []
    @children = []
    @parent = nil
  end

  def to_s
    name
  end

  alias inspect to_s

  def add_product p
    if @children.empty?
      @products << p
      p.parent_categories << self
    end
  end

  def add_category c
    if @products.empty? and not c.parent
      @children << c
      c.parent = self
    end
  end

  def all_products
    if @children.empty?
      @products
    else
      @children.reduce [] { |acc, c| acc.concat c.all_products }
    end
  end

end

Example usage.

food = Category.new 'food'
gsf = Category.new 'gas station food'
ff = Category.new 'fast food'
sandwich = Product.new 'sandwich'
pizza = Product.new 'pizza'

food.add_category gsf
food.add_category ff
gsf.add_product sandwich
ff.add_product pizza

puts "sandwich.categories = #{sandwich.categories}"
puts "pizza.categories = #{pizza.categories}"
puts "food.all_products = #{food.all_products}"

Gives.

sandwich.categories = [gas station food, food]
pizza.categories = [fast food, food]
food.all_products = [sandwich, pizza]

Click here for an explanation of the reference implementation.

1. Each product has a name.

We create a class of products.

class Product

  attr_reader :name

  def initialize name
    @name = name
  end

  def to_s
    @name
  end

  alias inspect to_s

end

Example usage.

sandwich = Product.new 'sandwich'
puts "sandwich = #{sandwich}"
puts "[sandwich] = #{[sandwich]}"

Gives.

sandwich = sandwich
[sandwich] = [sandwich]

2. Each category has a name.

We create a class of categories.

class Category

  attr_reader :name

  def initialize name
    @name = name
  end

  def to_s
    name
  end

  alias inspect to_s

end

Example usage.

gsf = Category.new 'gas station food'
puts "gsf = #{gsf}"
puts "[gsf] = #{[gsf]}"

Gives.

gsf = gas station food
[gsf] = [gas station food]

3. Each product may belong to one or more categories.

Given a category, we record the products that belong to the category in array Category#@products. We append products to a category by means of method Category#add_product.

class Category

  attr_reader :name, :products

  def initialize name
    @name = name
    @products = []
  end

  ...

  def add_product p
    @products << p
  end

end

Example usage.

gsf.add_product sandwich
puts "gsf.products = #{gsf.products}"

Gives.

gsf.products = [sandwich]

4. Each category may have subcategories.

Given a category, we record the children categories in array Category#@children. We append subcategories by means of method Category#add_category.

class Category

  attr_reader :name, :products, :children

  def initialize name
    @name = name
    @products = []
    @children = []
  end

  ...

  def add_category c
    @children << c
  end

end

Example usage.

food = Category.new 'food'
food.add_category gsf
puts "food.children = #{food.children}"

Gives.

food.children = [gas station food]

5. Categories that have products do not have subcategories.

This is a constraint on relations _belongs-to_ and _subcategory_. We constraint each relation by constraining corresponding methods Category#add_product and Category#add_category.

class Category

  ...

  def add_product p
    @products << p if @children.empty?
  end

  def add_category c
    @children << c if @products.empty?
  end

end

Example usage.

ff = Category.new 'fast food'
gsf.add_category ff
puts "gsf.children = #{gsf.children}"

pizza = Product.new 'pizza'
food.add_product pizza
puts "food.products = #{food.products}"

Gives.

gsf.children = []
food.products = []

6. Each category has at most one parent.

This is a constraint on relation _subcategory_. We apply the constraint by constraining method Category#add_category. We create instance variable Category#@parent to label each category with its parent.

class Category

  attr_reader :name, :products, :children
  attr_accessor :parent

  def initialize name
    @name = name
    @products = []
    @children = []
    @parent = nil
  end

  ...

  def add_category c
    if @products.empty? and not c.parent
      @children << c
      c.parent = self
    end
  end

end

Example usage.

gsg = Category.new 'gas station goods'
gsg.add_category gsf
puts "gsg.children = #{gsg.children}"
puts "gsf.parent = #{gsf.parent}"

Gives.

gsg.children = []
gsf.parent = food

7. You may ask a product for its corresponding categories.

This rule asks for those categories that are ancestors of a given product in relation _subcategory_. We compute the ancestor categories by method Product#categories. For a given product, the computation starts from the categories that contain the product. Those categories are recorded in array Product#@parent_categories. The array is populated by method Category#add_product.

class Product

  attr_reader :name
  attr_accessor :parent_categories

  def initialize name
    @name = name
    @parent_categories = []
  end

  ...

  def categories
    @parent_categories.reduce [] do |acc, c|
      begin
        acc << c
        c = c.parent
      end while c
      acc
    end
  end

end

class Category

  ...

  def add_product p
    if @children.empty?
      @products << p
      p.parent_categories << self
    end
  end

  ...

end

Example usage.

puts "sandwich.categories = #{sandwich.categories}"

Gives.

sandwich.categories = [gas station food, food]

8. You may ask a category for its corresponding products.

This rule asks that we collect the products of categories that are descendant of a given category in relation _subcategory_. We do so by traversing relation _subcategory_ from the given category all the way down to leaf descendants. We do the traversal and collect corresponding products by method Category#all_products.

class Category

  ...

  def all_products
    if @children.empty?
      @products
    else
      @children.reduce [] { |acc, c| acc.concat c.all_products }
    end
  end

end

Example usage.

food.add_category ff
ff.add_product pizza
puts "food.all_products = #{food.all_products}"

Gives.

food.all_products = [sandwich, pizza]

Other uses of WITH clauses

Apply several data modifications in the same query (section 7.8.2).
Apply recursive self-references in a data-modifying query (section 7.8.2).

The Category Problem: graph traversal by recursive SQL queries

Problem

Solution

Database schema

Recursive queries

Reference implementation in Ruby

Other uses of WITH clauses

Comments