Maximum Number of Points on a Line
Given n points on a 2D plane, find the maximum number of points that lie on the same straight line. For example, consider the following points.
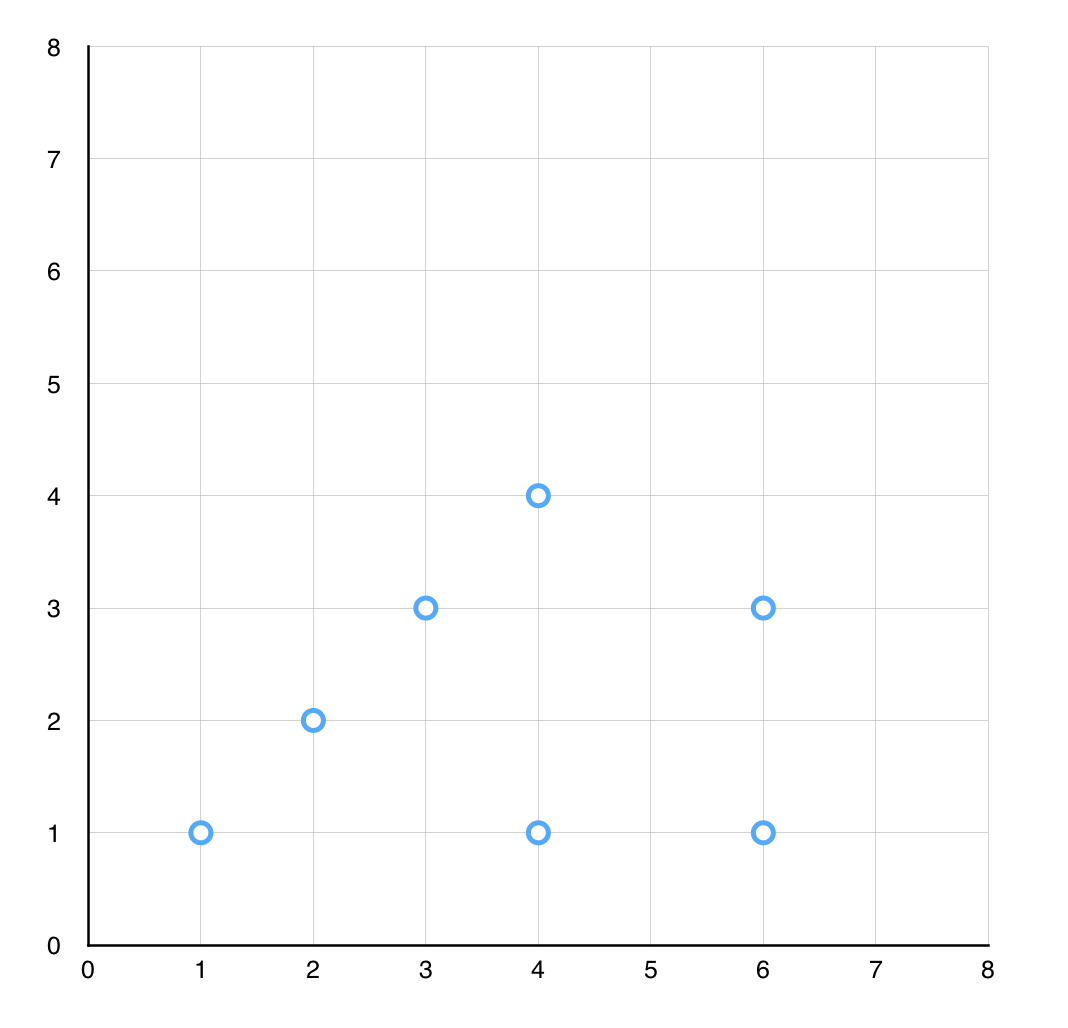
The maximum number of points over the same straight line is 4. Those points are (1,1), (2,2), (3,3), and (4,4).
Input.
The first line consists of an integer, n, that indicates the number of points
you will be given.
Each of the following n lines consists of a pair of integers separated by one or more spaces
corresponding to the x and y components of a point.
Consider the following example.
7
1 1
2 2
3 3
4 4
4 1
6 1
6 3Output.
The output consists of a single number, the maximum number of points that lie on the same straight line. For the example input, the maximum is 4.
Solution
Here is a Ruby implementation.
def mpoal pp
m = if pp.length > 0 then 1 else 0 end
pp.each_with_index do |a, i|
break if m >= pp.length - i
buckets = {}
max_bucket = 0
count_a = 1
pp[i+1..-1].each do |b|
if b[0] - a[0] == 0
slope = :inf
else
slope = (b[1].to_f - a[1]) / (b[0].to_f - a[0])
end
if a == b
count_a += 1
else
buckets[slope] = 0 if not buckets.has_key?(slope)
buckets[slope] += 1
max_bucket = [max_bucket, buckets[slope]].max
end
m = [m, count_a + max_bucket].max
end
end
return m
end
def main
n = readline.to_i
pp = []
while n > 0
p = readline.strip.split(' ').map{ |c| c.to_i }
pp << p
n -= 1
end
puts mpoal(pp)
end
main