You are given a string and a set of letters. Your task is to return any shortest substring that consists of all and only the letters in the set.

Edit 2018-02-04: Created new section Problem Structure, revisited section Approach, and explained solution algorithm instead of just inserting the solution implementation.

Edit 2017-04-02: The example string did not correspond to the illustrations. Thanks to Guillermo Cruz for the correction.

Consider string aabbxbbcaab and the set of letters {a,b,c}. The only possible answer is bca as illustrated in the following diagram.

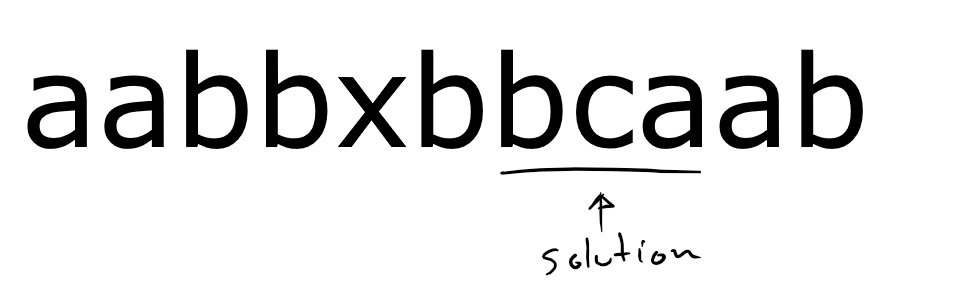
When there is no shortest substring, return the empty string.

Input. The input consists of one or more cases. Each case consists of two strings, one on a separate line. The first string is the string where you will search for a shortest substring. The second string indicates the characters in the set. The input is terminated by EOF. The following is a sample input file.

xaabbca
abc
aabxbcbaaccb
abc
aabbccbbabbcaabcbc
abc

Output. For each input case, print on a single line a shortest substring or the empty string. The following is the output file that corresponds to the sample input file.

bca
cba
bca

Problem Structure

Given an input pair of set and string, the structure of the string consists of solutions, candidate solutions, and pre-candidate solutions.

A solution is a shortest candidate solution we find in the string. When there are no candidate solutions, the solution is the empty string.

For a given prefix, a candidate solution is the shortest prefix made of all and only the allowed letters. There may not be a candidate solution for every prefix. For example, consider the candidates for string aabbxbbcaab in the following diagram.

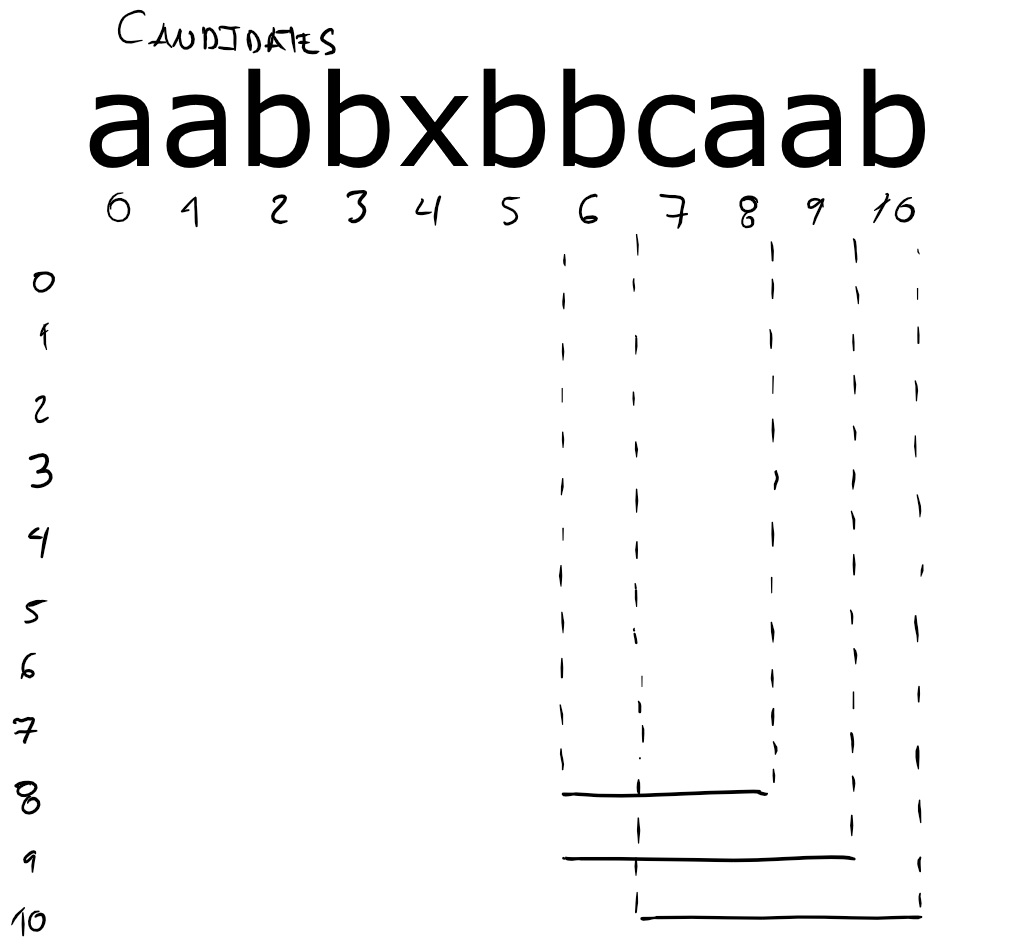
The meaning of the diagram is the following. There is a numbered row for each prefix of the string. Each horizontal line corresponds to a candidate. Each horizontal line indicates the substring that constitutes the corresponding candidate. For the prefix that ends in position 8, the candidate solution is the substring bca. That substring runs from position 6 to position 8. That prefix is also the solution. For the prefix that ends in position 7, there is no candidate because every prefix that includes all allowed letters also includes the forbidden letter x.

For a given prefix, a pre-candidate solution is the shortest suffix that contains as many allowed letters as possible. For example, consider the pre-candidates for string aabbxbbcaab in the following diagram.

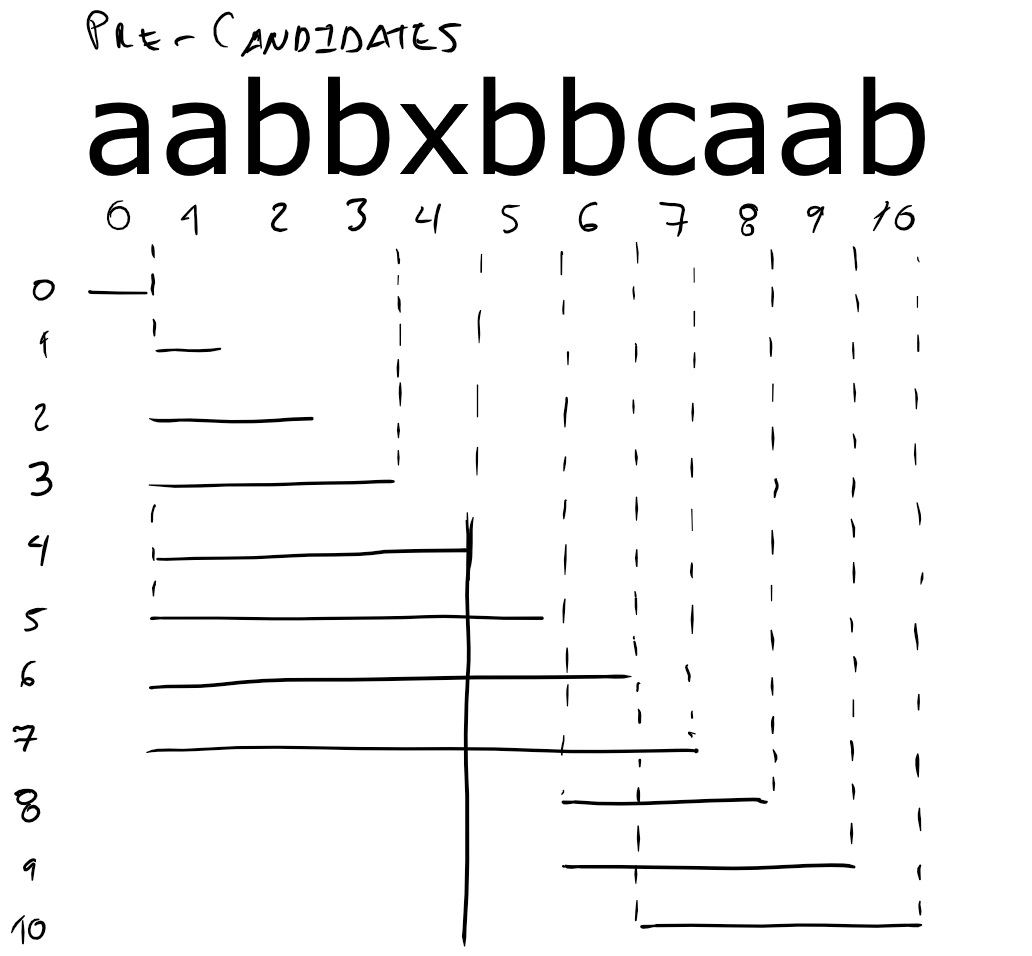
The meaning of the diagram is the following. There is a numbered row for each prefix of the string. Each horizontal line corresponds to a pre-candidate. The vertical solid line indicates the position of forbidden letter x. For the prefix that ends in position 8, the pre-candidate is the substring bca. For the prefix that ends in position 7, the pre-candidate is the substring that begins at position 1 and ends in position 7, even though that substring contains the forbidden letter.

Approach

Our approach consists in computing pre-candidates, selecting candidates, and selecting the shortest candidate.

We compute pre-candidates in the following way. We consider each prefix. For the prefix, we compute the last position of each allowed letter. The beginning of the pre-candidate is the minimum of those positions. The end of the pre-candidate is the end of the prefix. For example, consider letter positions and pre-candidates for string aabbxbbcaab in the following diagram.

The meaning of the diagram is the following. There is a numbered row for each prefix of the string. Each horizontal line corresponds to a pre-candidate. The letter a on the first row also corresponds to a pre-candidate. For a given row, each allowed letter indicates the last position of the letter within the corresponding prefix. The vertical solid line indicates the position of forbidden letter x. For the prefix that ends at position 7, the minimum position of allowed letters is 1 and thus 1 is the beginning of the corresponding pre-candidate.

We select candidates from pre-candidates in the following way. We reject those pre-candidates that satisfy any of the following two conditions.

1. The pre-candidate contains a forbidden letter.
2. The pre-candidate does not contain all allowed letters.

For example, consider the previous diagram of letter positions and pre-candidates. All pre-candidates for prefixes 0 to 7 are not candidates. For prefixes 0 to 6 the reason is that they lack letter c. For prefix 7 the reason is that the pre-candidate contains letter x. We keep pre-candidates for prefixes 8 to 10.

For a given pre-candidate, we determine that it satisfies any of the conditions by applying the following two rules.

1. A pre-candidate has a forbidden letter when the last position of any forbidden letter is after the beginning of the pre-candidate. For example, the pre-candidates that intersect the solid vertical line in the previous diagram have forbidden letter x after the beginning and are thus rejected.
2. A pre-candidate does not contain all allowed letters when the count of last positions is not the same as the count of allowed letters. For example, consider the row for the prefix that ends in position 3. The count of last positions is 2 and the pre-candidate is thus rejected.

We select the shortest candidate after selecting all candidates. For example, consider the previous diagram. Out of the three candidates (prefixes 8 to 10) we select the candidate corresponding to prefix 8 as the solution.

Algorithm and Implementation

Our solution algorithm consists in placing a window over each pre-candidate from left to right, applying to the window the two rules for selecting candidates, and updating the current solution when the window is better. To illustrate our algorithm, consider the following implementation in Ruby.

 1: #!/usr/bin/env ruby
 2: 
 3: def shortest_substring_of_allowed_letters s, allowed
 4:   last = allowed.chars.map { |c| [c, -1] }.to_h
 5:   allowed_count = 0
 6:   min_left = min_right = left = forbidden_last = -1
 7:   min_length = s.length + 1
 8:   s.chars.each_with_index do |c, right|
 9:     if last.has_key? c
10:       allowed_count += 1 if last[c] <= forbidden_last
11:       last[c] = right
12:       while last[s[left]] != left
13:         left += 1
14:       end
15:       length = right - left + 1
16:       if allowed_count == last.size and length < min_length
17:         min_length = length
18:         min_left = left
19:         min_right = right
20:       end
21:     else
22:       forbidden_last = right
23:       allowed_count = 0
24:     end
25:   end
26:   if min_length < s.length + 1
27:     return s[min_left..min_right]
28:   else
29:     return ''
30:   end
31: end
32: 
33: while true
34:   a = readline.strip rescue break
35:   b = readline.strip rescue break
36:   puts shortest_substring_of_allowed_letters a, b
37: end

In our implementation, parameters s and allowed on line 3 are Ruby arrays.

Placing a window over each pre-candidate consists of moving its boundaries left and right over string s. We move right in the main loop of the algorithm without any restriction. The crucial aspect of the algorithm is moving left.

Moving left consist in keeping track of the last position of allowed letters and moving left to the right until we reach the leftmost position (lines 11-14).

We keep track of last position of each allowed letter in the following way. When the letter at right is allowed, we know that this is the last position of the letter and we store the position in dictionary last (line 11). For example, consider the following diagram that we already considered in the previous section.

When we move the right boundary to the first position, we know that the last position of a is 0 and nothing more, so last contains only the position of a. When we move to position 1, we update the position of a to 1. At position 2 we find the first occurrence of letter b and at position 3 we set last['b'] = 3.

We move left to the leftmost position in last by moving left to the right until left is the last position of an allowed letter (lines 12-14). This works because every time we move right, either the leftmost position in last changed or not. When the leftmost position changed, it is located to the right of left. For example, consider the computation of left for the prefix that ends in position 8 illustrated by the following diagram.

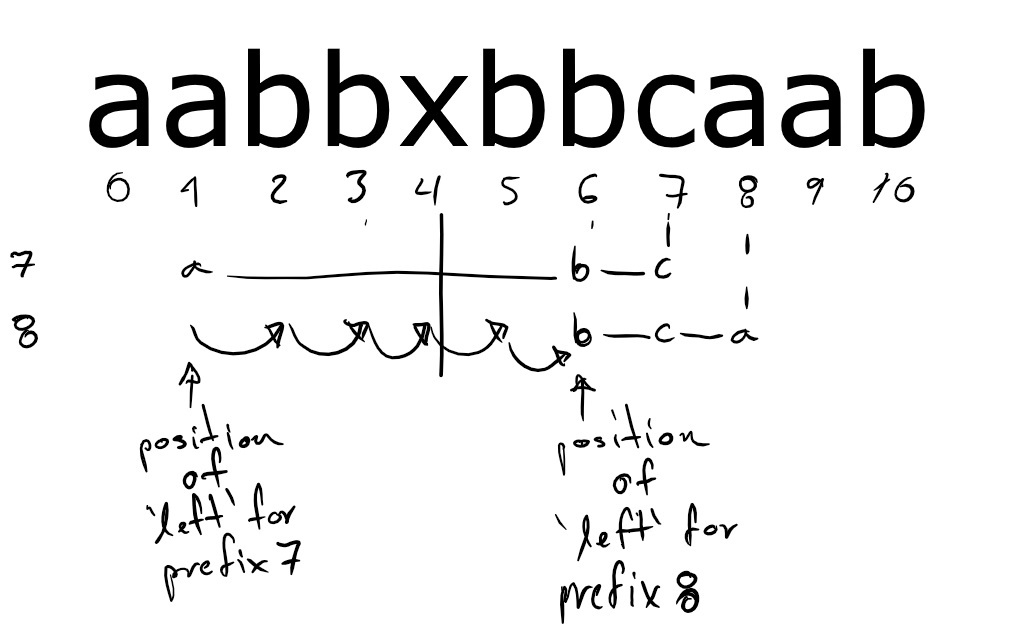
Because the last position of a changes, we move left to the right until we reach the last position of b.

Applying the two rules for candidates given in the previous section consists in counting the number of allowed letters after the last forbidden letter. For that reason, when we move the right boundary to a forbidden letter, we reset the count of allowed letters after the last forbidden letter allowed_count and we register the position in forbidden_last (lines 22-23). When we move the right boundary over an allowed letter, we only increment allowed_count when the previous last position of the letter is before the last forbidden letter (line 10).

Updating solution consists in checking that all the allowed letters happen after the last forbidden letter and that the length of the window is smaller than the previous solution (lines 15-20).

The run time of this algorithm is $@O(|s|)@$ because both window boundaries move from left to right. For boundary left, the number of iterations of the nested loop in lines 12-14 is bounded by the length of string s.

Comments