Write a function that merges two sorted integer arrays using no other buffer than the one you are given.

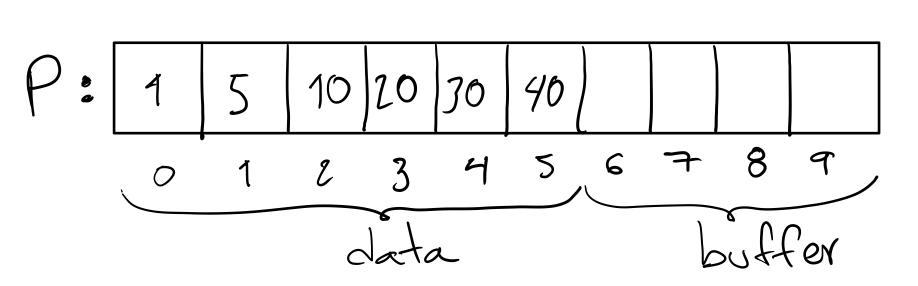
One of the arrays consists of data and an empty space called buffer. This array is the primary array because this is where you will store the result of the merge. Even though the buffer contains integers, we consider it empty. Consider the following example primary array P.

The other array is at most the size of the buffer and consists of data. This array is the secondary array because it contains the elements that you will merge into the primary array. Consider the following example secondary array S that corresponds to the example primary array.

The expected final state of P given S is the following.

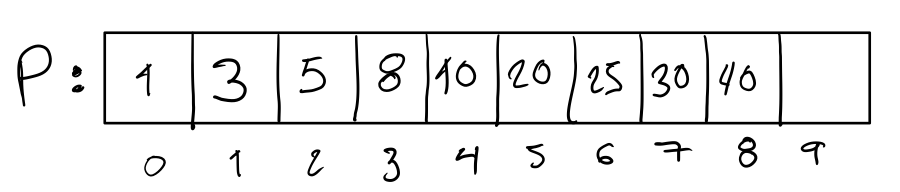
The integer of position 9 in the final state is unspecified because we do not care about what’s beyond the length of the result of the merge.

Input. The input to your function consists of a reference to the principal array, a reference to the secondary array, and the length of the data. For example, for the example primary and secondary arrays, the length of the data is 6.

Output. The output of your function consists of the expected final state of the primary array and the length of the merge. Given that the final state of the primary array is available through any reference to the array, the only return value of your function is the length of the merge. For example, for the example primary and secondary arrays, the length of the merge is 9.

Solution

We merge data and the secondary array by copying their elements from right to left in descending order. We write the elements in the primary array from right to left starting from the last position.

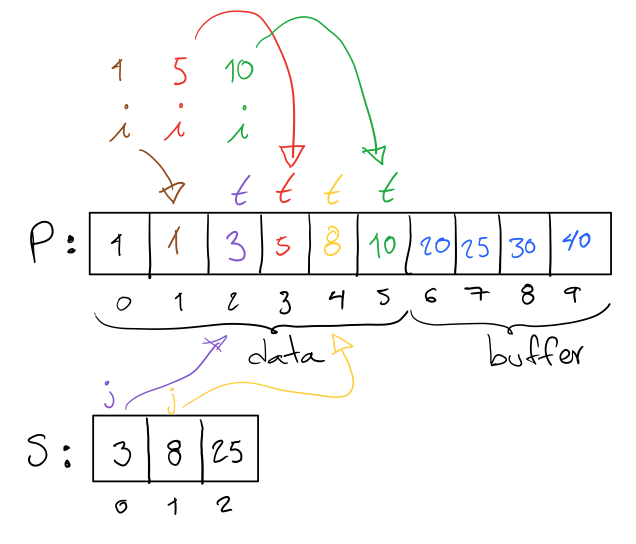
To illustrate the procedure, consider the following diagram of the example primary and secondary arrays.

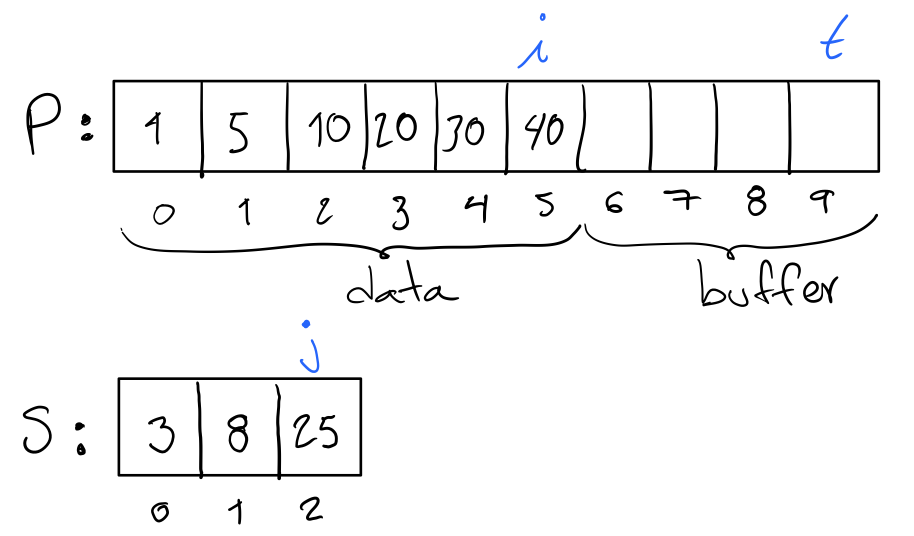
Position i corresponds to the last element of the data. Position j corresponds to the last element of the secondary array S. Position t is the last position in the primary array P.

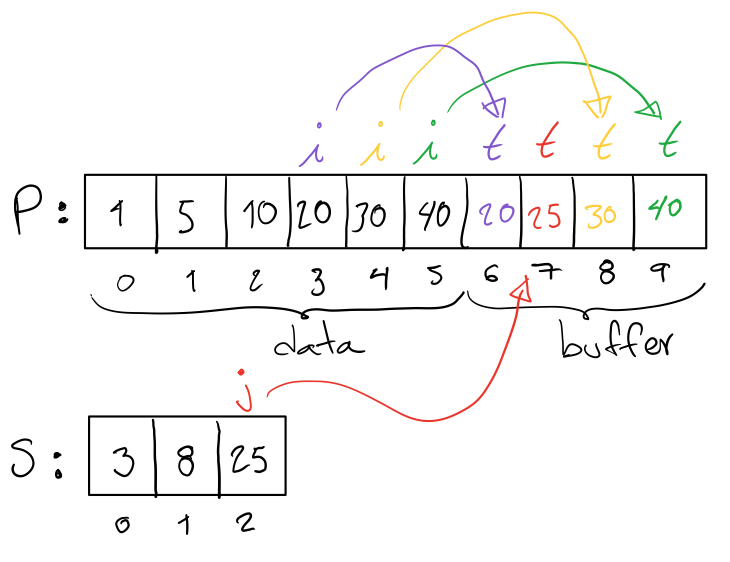
Given positions i, j, and t, we write the last four elements of the result as illustrated by the following diagram. The order we follow is green, yellow, red, and purple.

For the rest of the result, we continue with the merge of data and the secondary array in descending order. In doing so, we overwrite positions 1 to 5 of the primary array P.

After the merge, we shift the result to the right and thus obtain the following final state of P.

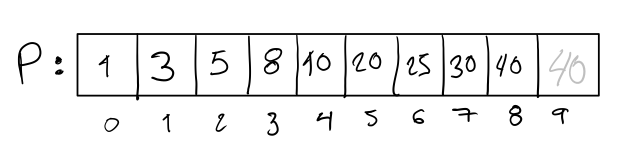
Implementation

We implement the solution in Ruby as follows.

def merge_by_buffer p, s, l
  i = l - 1
  j = s.length - 1
  t = p.length - 1
  while i >= 0 or j >= 0
    if i >= 0 and j >= 0
      if p[i] > s[j]
        p[t] = p[i]
        i -= 1
      else
        p[t] = s[j]
        j -= 1
      end
    elsif i >= 0
      p[t] = p[i]
      i -= 1
    else
      p[t] = s[j]
      j -= 1
    end
    t -= 1
  end
  t += 1
  h = 0
  while t < p.length
    p[h] = p[t]
    h += 1
    t += 1
  end
  return h
end

Comments