Print all strings consisting of n balanced parentheses.

Edit 2017-05-17. Added implementation in Golang.

For example, the strings consisting of three balanced parentheses are the following.

()()()
()(())
(())()
(()())
((()))

Input. The input consists of a sequence of numbers, one on a line of its own, followed by EOF. The following is an example input.

1
0
3
2

Output. For a given input, the output consists of one of more sequences of balanced parentheses strings. Each sequence corresponds to a number in the input. The sequences appear in the order determined by the input numbers. Each sequence need not be sorted. The strings that belong to a given sequence must not be repeated. For example, the following is the output that corresponds to the previous example input.

()

()()()
()(())
(())()
(()())
((()))
()()
(())

Solution

The structure of any given string consisting of n balanced parentheses obeys the following three rules.

Rule 1. The first position in the string consists of an opening parenthesis.

Rule 2. A given position in the string may consist of an opening parenthesis when there are less than n opening parentheses in the previous positions. For example, consider the fourth position of the following string.

(()())
123456
   ^

The opening parentheses at the fourth position is allowed because there are only 2 opening parentheses in prefix (().

Rule 3. A given position in the string may consist of a closing parenthesis when there is an unmatched opening parenthesis at some previous position. For example, consider the fourth position of the following string.

(())()
123456
   ^

The closing parenthesis at position 3 is allowed because the opening parenthesis in the first position is unmatched in prefix (().

Our approach to enumerating all balanced parentheses strings of length n consists in applying the rules from left to right until we output n pairs of parentheses and then backtracking at each position where more than one option is possible. To illustrate our approach, consider the following tree of rule applications for n = 3.

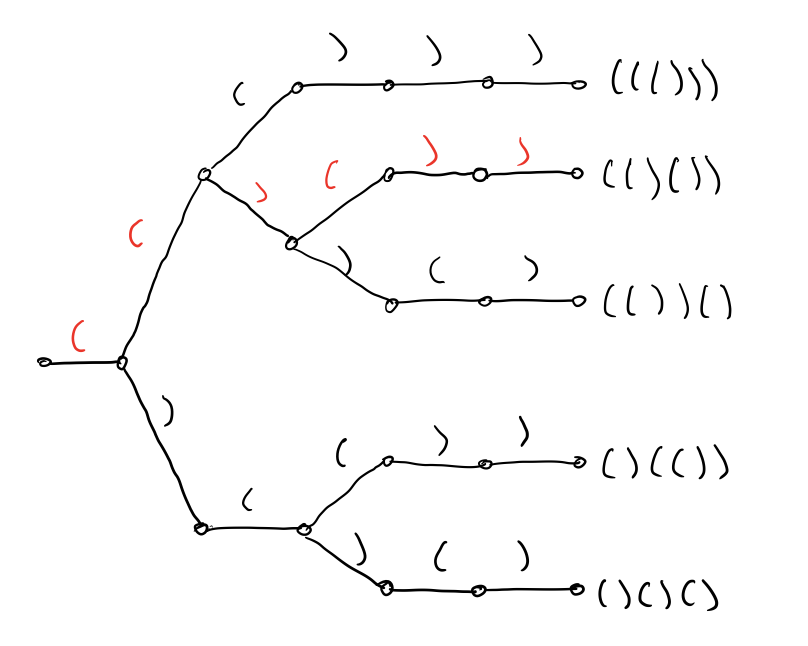
Consider the path highlighted in red. The path leads to the following string.

(()())
123456

The first position of the string corresponds to the first transition from left to right and also to Rule 1. The second position may be an opening or closing parenthesis, so we choose an opening parenthesis. For the third position we have the same choices, so we choose a closing parenthesis. Something similar happens for the fourth position. At this point, the last two positions must be closing parenthesis because we have used 3 opening parentheses and there are two unmatched opening parentheses in prefix (()(.

To apply the rules correctly, we remember the number of opening parenthesis still available and the number of unmatched opening parenthesis as we build each string from left to right. To illustrate the building of each string, we decorate each transition of our previous tree with the number of opening parenthesis available to the next node. On top of that number, we write the number of unmatched opening parenthesis for the next node.

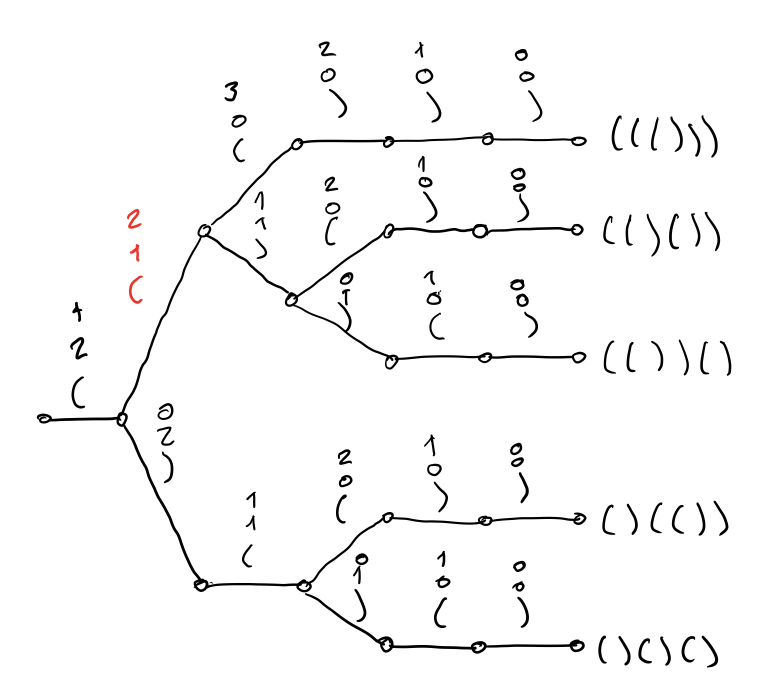
Consider the transition highlighted in red. In that transition, number 2 indicates that there are 2 unmatched parentheses available to the next node and number 1 indicates that there is 1 more opening parenthesis available to the next node.

Implementation

We implement the application of rules in Ruby and Golang.

Our Ruby implementation is the following.

#!/usr/bin/env ruby

def e l, r, s, e_n
  if l > 0
    e (l - 1), (r + 1), (s + '('), e_n
  end
  if r > 0
    e l, (r - 1), (s + ')'), e_n
  end
  if l == 0 and r == 0
    e_n << s
  end
  return e_n
end

while true
  n = readline.strip.to_i rescue break
  puts e n, 0, '', []
end

Our Golang implementation is the following. You will find a corresponding Makefile here.

package main

import (
  "bufio"
  "os"
  "fmt"
  "strconv"
)

func e(l, r int, s string, e_n []string) ([]string) {
  if l > 0 {
    e_n = e(l - 1, r + 1, s + "(", e_n)
  }
  if r > 0 {
    e_n = e(l, r - 1, s + ")", e_n)
  }
  if l == 0 && r == 0 {
    e_n = append(e_n, s)
  }
  return e_n
}

func main() {
  scanner := bufio.NewScanner(os.Stdin)
  for scanner.Scan() {
    n, err := strconv.Atoi(scanner.Text())
    if err != nil { break }
    o := e(n, 0, "", make([]string, 0, 1))
    for _, s := range o {
      fmt.Printf("%s\n", s)
    }
  }
}

Comments