Given a binary search tree, print all possible arrays that produce the tree. An array produces a tree by inserting the array’s elements one by one into the tree. The elements are taken from the array from left to right.

Example. Consider the following binary search tree.

   4
  / \
 2   9

Its corresponding arrays are the following.

[4, 9, 2]
[4, 2, 9]

Input. The input file consists of positive integer N on the first line followed by N test cases. The first line of any given test case consists of a pair of positive integers M and R separated by a single space. Integer M indicates the number of edges in the binary search tree and R is the root of the tree. The M lines that remain in the test case consist of pairs of positive integers P and C corresponding to an edge that goes from parent node P to child node C. The following input file corresponds to the example.

1
2 4
4 2
4 9

Output. The output consists of all possible arrays for each test case. The arrays that correspond to a given test case must appear in lexicographical order. Each array must appear on a single line. To print an array, print the elements separated by space. For example, the corresponding is the output for the previous input.

4 2 9
4 9 2

Solution

We build each array from left to right by choosing for every position one node out of a set of possible choices for that position. The set of possible choices for a position is given by the corresponding array prefix. We illustrate the method with the following tree.

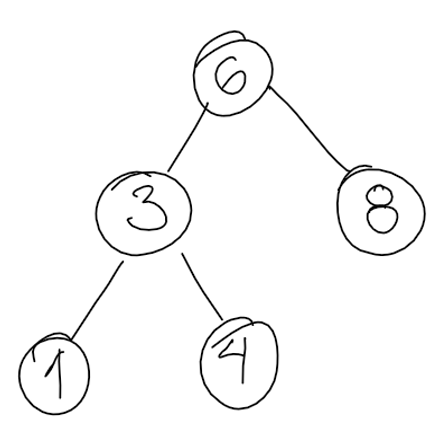
We visit the tree starting from the root node. We create array $@acc_0@$. We collect the children of the root in set $@cho_0@$ as possible choices to visit next. The state is the following.

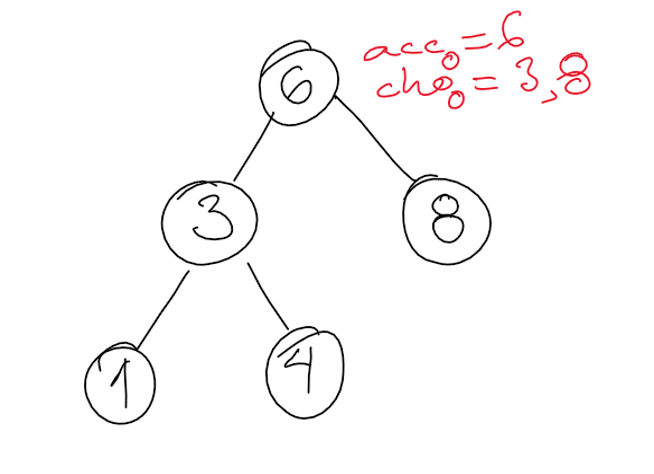
We choose to visit node 3 next. We append 3 to the end of $@acc_0@$ and label the new array $@acc_1@$. We remove 3 from set of choices $@cho_0@$, add the children of 3, and label the new set as $@cho_1@$. The state is the following.

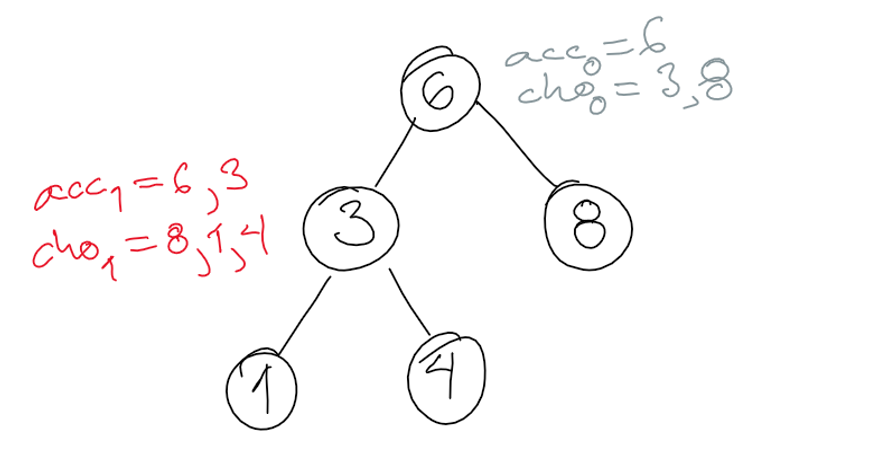
We choose to visit node 8 next. We append 8 to the current array and label the result $@acc_2@$. We remove 8 from the set of choices and label the result $@cho_2@$. The state is the following.

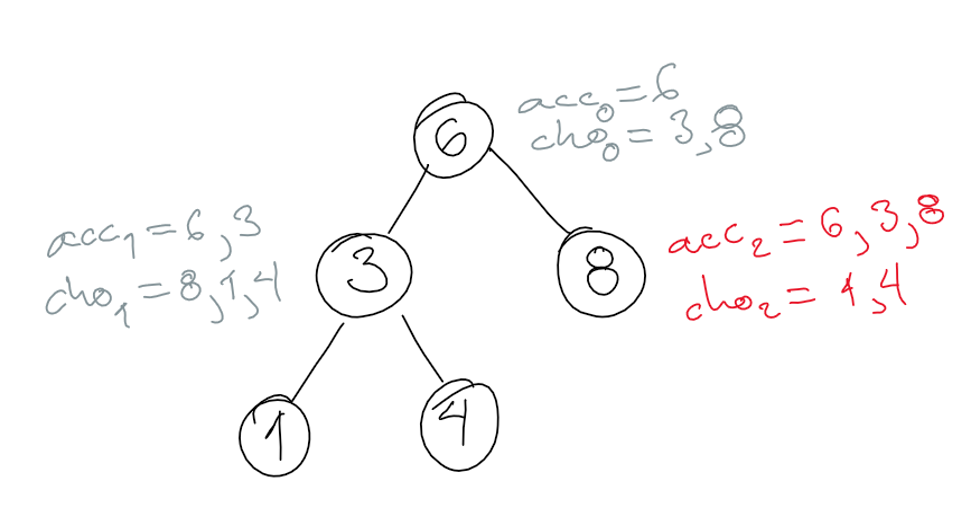
We choose to visit node 1 next. The state is the following.

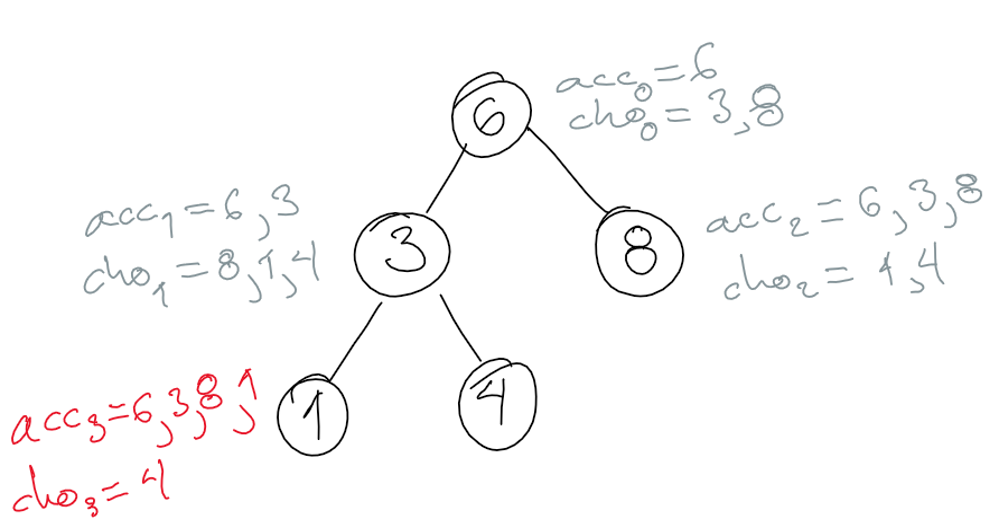
We choose to visit node 4 next. There are no further choices. We have our first possible array. The state is the following.

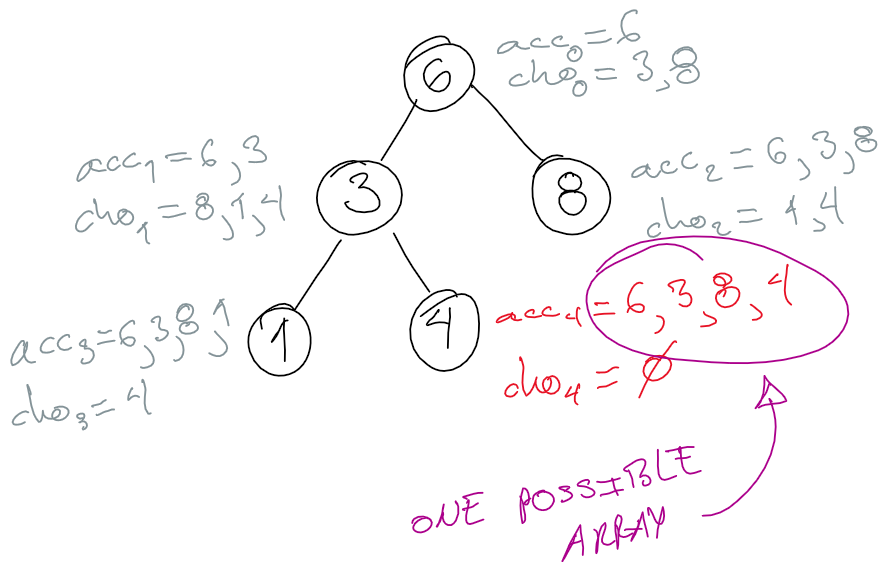
To generate the rest of the possible arrays, we backtrack until we can make a different choice and apply the method again.

Implementation

Here is a Ruby implementation.

#!/usr/bin/env ruby

def apa children, cho, acc, curr
  children[curr].each { |c| cho[c] = 1 } if !!children[curr]
  r = []
  if cho.empty?
    r << acc + [curr]
  else
    cho.keys.each do |k|
      cho.delete(k)
      acc.push curr
      r += apa(children, cho, acc, k)
      acc.pop
      cho[k] = 1
    end
  end
  children[curr].each { |c| cho.delete c } if !!children[curr]
  return r
end
        

def main
  n = readline.to_i

  while (n -= 1) >= 0
    m, r = readline.strip.split(' ').map(&:to_i)
    children = {}
    while (m -= 1) >= 0
      p, c = readline.strip.split(' ').map(&:to_i)
      children[p] ||= []
      children[p] << c
    end
    apa(children, Hash.new, [], r).sort.each { |a| puts a.join(' ') }
  end
end

main

Comments