Travel Itinerary
Given the legs of an itinerary, determine the origin and destination of the trip.
For example, consider the following legs.
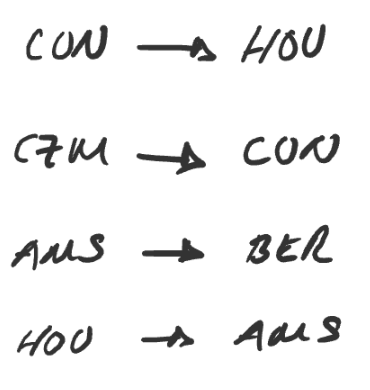
The origin for the trip is czm and the destination is ber.
Input.
The input begins with the number of legs n on a single line. The
next n lines consist of pairs of three letter identifiers, the
origin and destination for the given leg. The legs always
correspond to an origin, zero or more intermediate places, and a
destination. The following is an example
input.
4
cun hou
czm cun
ams ber
hou amsOutput. The output consists of the three letter identifiers for the origin and destination for the whole trip on a single line and separated by a single space. The following is the output that corresponds to the example input.
czm berNaive approach
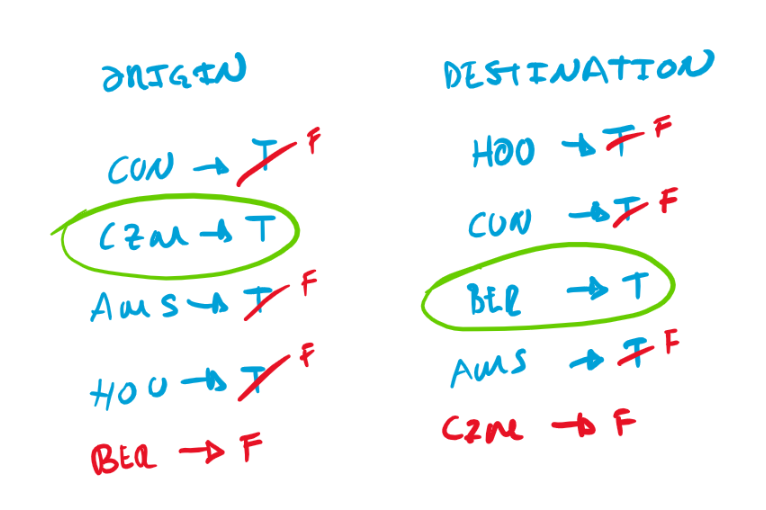
A naive approach consists of building a list of candidates for origin/destination, eliminating candidates, and selecting the candidate origin/destination that remains. Consider the following legs.

Candidates. We collect in dictionary origin the origin of each
leg. We set each origin to true to indicate that each one is a
possible origin. We do the same with the destinations.

Elimination. We then consider each leg. For each destination, we
set the corresponding value in origin to false to indicate that that
place is no longer a possible origin. We set each destination in
origin even if the place does not exist in origin, like in the
case of ber. We do the same for each origin.

Selection. Finally, we select the trip origin as the origin that remains set to true. We do the same for the destination.
The time complexity is O(E + V) where E is the number of legs and
V is the number of places in the trip. E is given by steps
Candidates and Elimination and V is given by Selection. But given
that V = E + 1 because all trips are a sequence of places from
origin to destination, the time complexity is in fact O(E). The
space complexity is O(V) because each dictionary may be at most
V elements.
Solution
We can trade step Selection of the naive approach for an additional pair of dictionaries without changing the time or space complexity in the following way.
Instead of collecting all candidate origins in a single dictionary and
then eliminating most of them, we keep possible origins in a dictionary
and places that are not origins in another. When we consider each
leg, we add the leg’s origin as a possible origin in dictionary
origin only when it does not already exist in dictionary
not-origin. Then, we add the leg’s destination to dictionary
not-origin so that we know the destination is not the trip origin.
Also, we remove the leg’s destination from dictionary origin because
the destination is not the trip origin. The following diagram
illustrates the process.
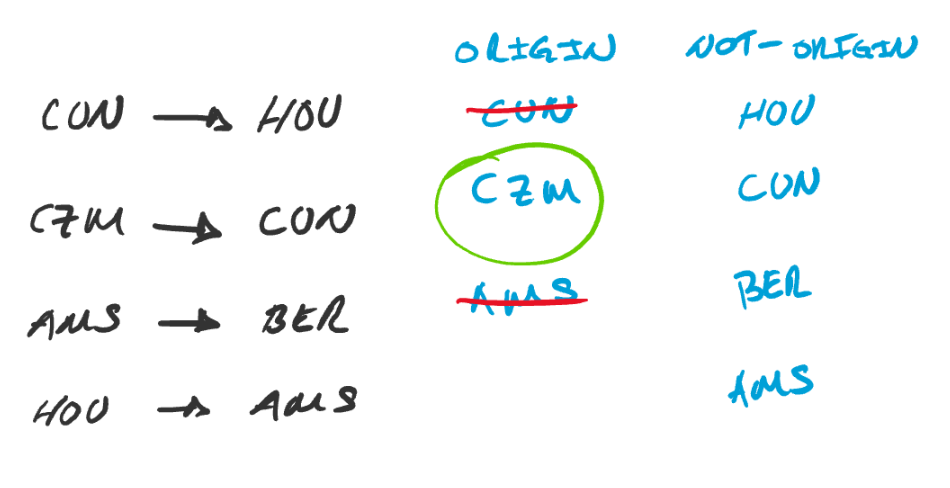
For each leg in the diagram, the corresponding origin and destination
are appended to their corresponding dictionary. When the origin
already exists in not-origin, we skip it. When the
destination was previously added to origin, we strike out its
occurrence in origin. After considering all legs, the origin is the
only element left in origin.
We do the same to find the trip destination. The following diagram illustrates the process.

The following is a Ruby implementation of the solution.
#!/usr/bin/env ruby
def find_origin_and_dest legs
origin = {}
not_origin = {}
dest = {}
not_dest = {}
legs.each do |o, d|
if !not_origin[o]
origin[o] = true
end
not_origin[d] = true
origin.delete d
if !not_dest[d]
dest[d] = true
end
not_dest[o] = true
dest.delete o
end
return origin.keys.first, dest.keys.first
end
def main
n = readline.to_i
legs = []
while n > 0
legs << readline.split(' ')
n -= 1
end
puts find_origin_and_dest(legs).join(' ')
end
mainThe time complexity is O(E). E is the number of legs. The space
complexity is O(V). V is the number of places.