When a pattern string occurs in a text, return the start index of the first occurrence.

For example, the index of the first occurrence of pattern abc in text ababcbbabc is 2 as illustrated in the following figure.

Input. The input consists of a text and a pattern string. The text is the first line of input and the pattern string is the second. The following is an example input.

ababcbbabc
abc

Output. The output consists of an integer without trailing or leading spaces, followed by a newline, followed by EOF. When the pattern occurs in the text, the integer is the index of the first occurrence. Otherwise, the integer is -1. The following example output corresponds to the example input.

2

Naive approach and implementation

Our naive approach consists in comparing from left to right the pattern against the text starting at each position until we find a match. For example, the following animation illustrates the approach for text ababaababacababacabc and pattern ababacabc.

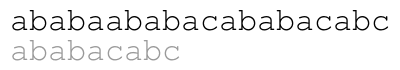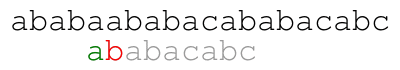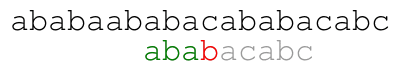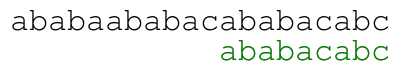
The following is a Ruby implementation of the approach.

#!/usr/bin/env ruby

def index_of pattern, text
  (0...text.length).each do |q|
    k = 0
    while k < pattern.length && q + k < text.length && pattern[k] == text[q + k]
      k += 1
    end
    return q if k == pattern.length
  end
  return -1
end

def main
  text = readline.strip
  pattern = readline.strip
  puts index_of pattern, text
end

main

The time complexity of the naive approach is $@O(n^2)@$, where $@n@$ is the length of the text, and the space complexity is $@O(1)@$.

Solution approach

Our solution approach is the following. We compare from left to right the pattern against the text starting from the first position. Every time the pattern does not match the text, we shift the pattern to the right to an offset where we already know that a prefix of the pattern matches the text and then continue comparing where we left off. For example, the following animation illustrates the approach for text ababaababacababacabc and pattern ababacabc.

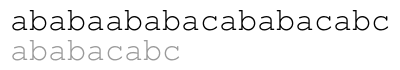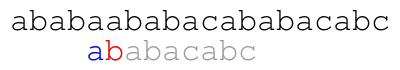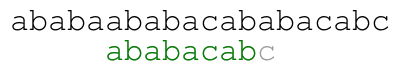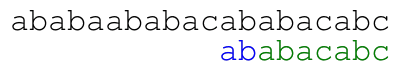
The meaning of the colors in the previous animation is the following. Each green letter is a letter that we just matched with the letter above. Each letter in blue is a letter that we already know matches the letter above upon shifting the pattern. Each red letter is a letter that we just found out that does not match the text.

We explain the approach by example over the previous text and pattern. The index of pattern in text is 11 as illustrated in the following figure.

Our approach begins in the following way. We compare the pattern against the text character by character from left to right until we either consume all characters of the pattern or we find a mismatch. The following animation illustrates the process.

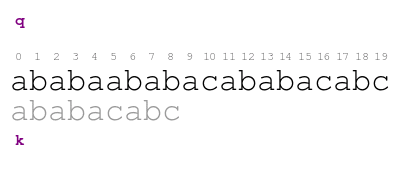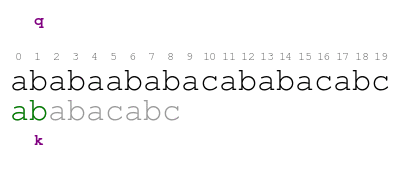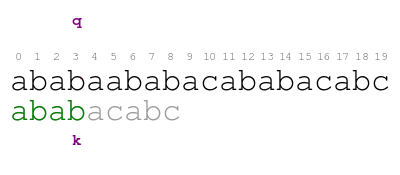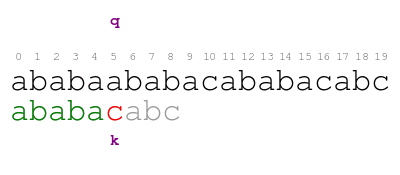
The meaning of the previous animation is the following. Letter q corresponds to the current character of the text. Letter k corresponds to the current character of the pattern. The comparison ends with a mismatch at position 5 of the text. Thus, the pattern does not match the text at the initial offset.

When we find the previous mismatch, we shift the pattern to the right to the smallest offset where the part of the pattern before position q already matches the text. Consider the pattern offsets from 1 to 5 in the following figure.

For offsets 1 and 3, the pattern prefix before position q does not match the text. The letters that do not match are marked in red. For offsets 2, 4, and 5, the pattern prefix before position q matches the text. The letters that match are marked in blue. Thus, we shift the pattern to offset 2 and also relocate k so that it coincides with q. The following figure illustrates the new position of the pattern and k upon shifting.

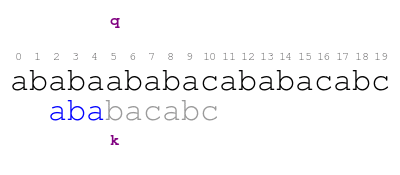
We resume comparing the pattern against the text and we immediately find the following mismatch.

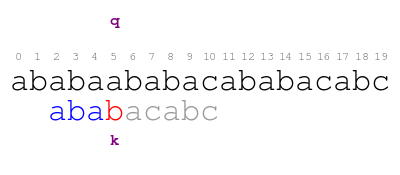
When we find the previous mismatch, the smallest offset that matches the text before q is 4. Thus, we shift the pattern to that offset and resume comparing the pattern against the text. We immediately find the following mismatch.

When we find the previous mismatch, the smallest offset that matches the text before q is 5. We shift again and compare. This time positions q and k match as follows.

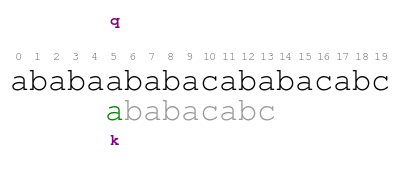
When we find a mismatch, we never consider smaller offsets than the current one or offsets greater than the current character of the text (position q). In the case of smaller offsets, we have already ruled out any smaller offsets by the time we reach the current offset. In the case of offsets greater than q, we must consider offset q before considering any of them.

The crucial aspect of shifting the pattern is figuring out the smallest offset that matches the text before position q. For that reason we annotate each pattern position with the longest pattern prefix that matches the text up to the position. The following animation illustrates the process for the first shift.

The meaning of the previous animation is the following. The numbers in purple are the annotations. We store annotations in list Pi. We only annotate positions before q because those are the only ones we may consider at this point of the whole example. For a given annotation, we never consider the prefix that ends at the position of the annotation. The annotation for the first position is 0 because the pattern prefix that matches the text before the first position is the empty prefix. For the second position, candidates are the empty prefix and the prefix of length 1. We rule out prefix of length 1 by shifting the pattern to offset 1 and thus annotate the second position of the pattern with 0. The annotation for the third, fourth, and fifth position is respectively 1, 2, and 3 because that is the longest prefix for each position. The last annotation indicates that the length of the longest pattern prefix that matches the text before position q is 3.

We apply Pi to shifting the pattern in the following way. When we find a mismatch at text position q, the annotation currently aligned with position q - 1 indicates the length of the longest pattern prefix that matches the text. Thus, we shift the pattern so that the prefix aligns with the text above. Consider the first shift in the following animation.

The meaning of the previous animation is the following. Given that q is at position 5 and the annotation at position 4 indicates prefix of length 3, the smallest offset we try next is 2.

We apply Pi to the second and third shifts as illustrated in the following animation.

After the last shift, we continue comparing the pattern against the text until we find another mismatch at position 13 as follows.

When we find the previous mismatch, we annotate the letters of pattern corresponding to text positions 10 to 12 in the following way.

We apply Pi to the last shift as illustrated in the following animation.

When the pattern is at offset 11, we compare the pattern against the text one last time and find that the pattern matches the text like so.

Computation of pattern annotations

For the purpose of simplifying our implementation of the solution approach, we separate concerns and compute the list of annotations Pi upfront.

It is possible to annotate the pattern upfront because the annotations are determined by the pattern alone. Every time we annotate the pattern on demand, the part of the text that we use is the same as the prefix of the pattern that we annotate. As an example, consider the annotations that we make after the first mismatch.

We explain the procedure by example over pattern ababacabc. Consider the following animation.

The procedure in the animation is the following. Letter k indicates the prefix we are currently annotating. Numbers in purple are annotations. Each position of k corresponds to a prefix of the pattern. The value of annotation at the end of prefix k indicates the longest proper prefix of k that is a suffix of k. The process always starts by annotating position 0 with value 0. For each subsequent position k, letter m indicates the current candidate proper prefix for k. When we match letters at k and m, we color letter m in green and move on. Otherwise, the next candidate for k is given by the annotation at m - 1. We shift the pattern to that candidate and check again. When we run out of candidates (i.e. m is 0), we annotate position k with 0.

The following is our implementation of the procedure in Ruby.

 1: def build_pi pattern
 2:   pi = Array.new(pattern.length, 0) # Array of zeroes of length |pattern|
 3:   m = 0
 4:   (1...pattern.length).each do |k|
 5:     while m > 0 && pattern[m] != pattern[k]
 6:       m = pi[m - 1]
 7:     end
 8:     if pattern[m] == pattern[k]
 9:       m += 1
10:     end
11:     pi[k] = m
12:   end
13:   return pi
14: end

The time complexity of build_pi is $@O(p)@$ where $@p@$ is the length of the pattern. The nested loop in lines 5 to 7 does not bump the time complexity because it executes at most $@O(p)@$ times. The nested loop shifts the pattern to the right and we can only shift the pattern at most $@p@$ times.

Implementation of solution approach

We explain the procedure that implements the solution approach by example over pattern ababacabc. Consider the following animation.

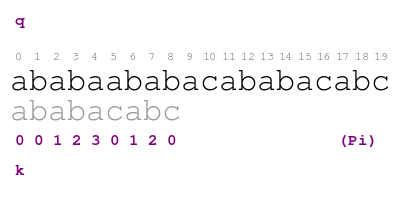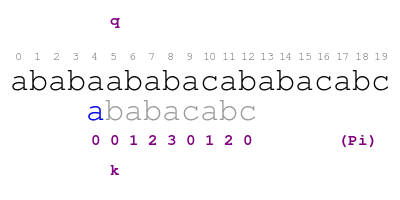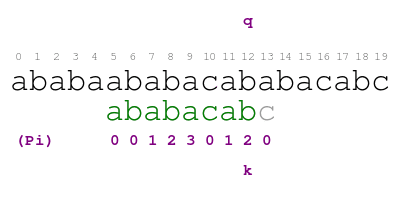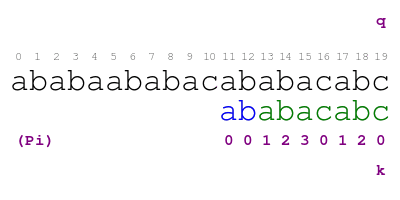
The procedure in the animation is the following. Letter q indicates the text character that we are currently matching with pattern character indicated by letter k. When there is a match, we color the pattern letter in green and move on. Otherwise, we shift the pattern so that we match the largest proper prefix of the pattern with the text before position q. We color the part of the prefix that match this way in blue. We find the prefix by looking at the annotation in position k - 1 of Pi. We repeat the process until positions q and k match or we run out of prefixes. We find a match of the pattern in text when we color each letter of the pattern in green or blue.

The following is our implementation of the solution approach in Ruby.

 1: def index_of pattern, text
 2:   pi = build_pi pattern
 3:   k = 0
 4:   (0...text.length).each do |q|
 5:     while k > 0 && pattern[k] != text[q]
 6:       k = pi[k - 1]
 7:     end
 8:     if pattern[k] == text[q]
 9:       return q - k if k + 1 == pattern.length
10:       k += 1
11:     end
12:   end
13:   return -1
14: end
15: 
16: def main
17:   text = readline.strip
18:   pattern = readline.strip
19:   puts index_of pattern, text
20: end
21: 
22: main

The time complexity of index_of is $@O(t + p)@$ where $@t@$ is the length of the text and $@p@$ is the length of the pattern. The nested loop in lines 5 to 7 does not bump the time complexity of index_of because it executes at most $@O(t)@$ times. The nested loop shifts the pattern to the right and we can only do that at most $@t@$ times. The time complexity is also $@O(t)@$ because $@t > p@$.

Knuth-Morris-Pratt Algorithm

Our implementation of the solution approach corresponds to the Knuth-Morris-Pratt Algorithm. The implementation is a transliteration of the pseudo-code in Section 32.4 of Cormen et al. You may want to refer to that section for a more rigorous and yet illustrative explanation of Knuth-Morris-Pratt Algorithm.

References

[Cormen et al]

Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009) [1990]. Introduction to Algorithms (3rd ed.). MIT Press and McGraw-Hill. pp. 1002-1012. ISBN 0-262-03384-4.

Comments