Shortest Substring That Contains Given Letters
You are given a string and a set of characters. Your task is to return any shortest substring that contains all the characters in the set.
Consider string 697581539 and the set of characters {1,5,9}.
The only possible answer is 1539 as illustrated in the following diagram.
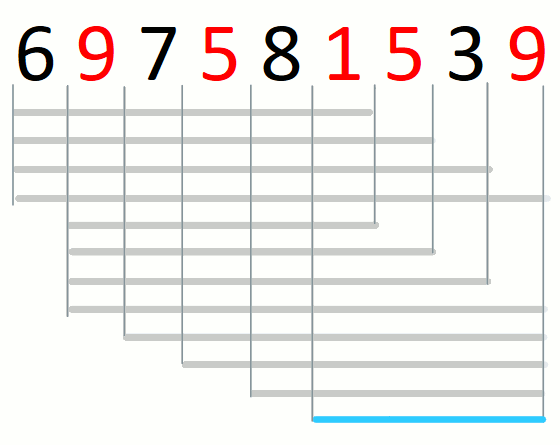
When there is no shortest substring, return the empty string.
Input. The input consists of one or more cases. Each case consists of two strings, each one on a separate line. The first string is the string where you will search for a shortest substring. The second string indicates the characters in the set. The input is terminated by EOF. The following is a sample input file.
697581539
159
figehaeci
hi
935185796
159Output. For each input case, print on a single line a shortest substring or the empty string. The following is the output file that corresponds to the sample input file.
1539
igeh
9351Problem Structure
Given an input pair of set and string, the structure of the string consists of solutions, candidate solutions, and pre-candidate solutions.
A pre-candidate solution is a substring that contains all characters
in the set. For example, consider the pre-candidate solutions for
string 697581539 and set {1,5,9}.
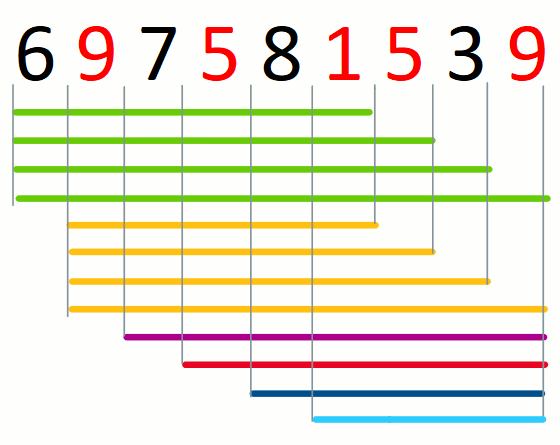
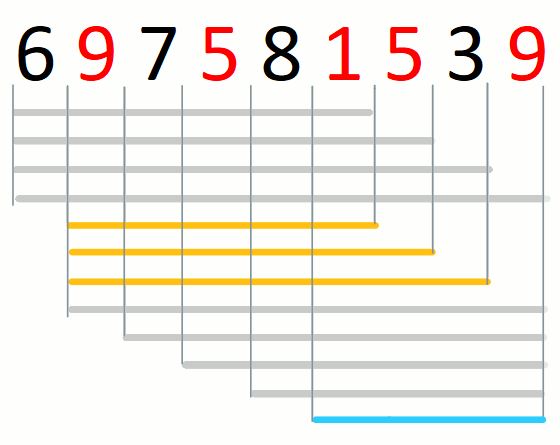
For a given prefix of the input string, a candidate solution is the
suffix that is a pre-candidate and shortest. There may not be a
candidate solution for a given prefix. For example. consider the
candidate solutions for string 697581539 and set {1,5,9}.
A solution is a shortest candidate solution in the string. When there
are no candidate solutions, the solution is the empty string. For
example, consider the solution for string 697581539 and set
{1,5,9}.

Approach
Our approach to the problem consists in finding the leftmost candidate
solution (if any) and transforming each candidate solution into the
next from left to right (if any). The process involves expanding and
contracting a
window.
The following animation illustrates the approach over string
697581539 and set {1,5,9}.
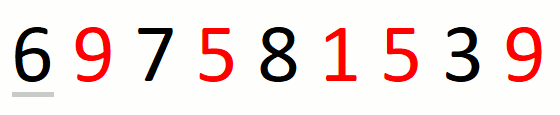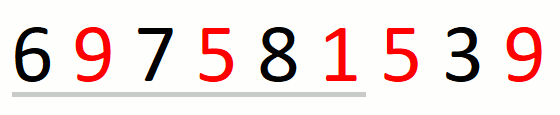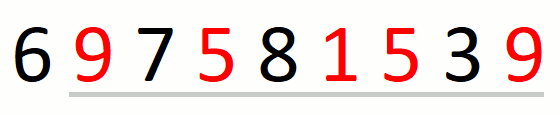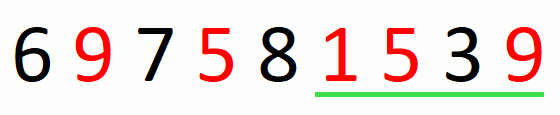
Finding the leftmost candidate consists in finding the leftmost
pre-candidate and refining it until we have the leftmost candidate.
For string 697581539 and set {1,5,9}, this part of the approach
is the following.
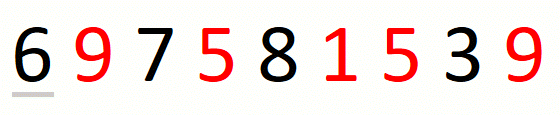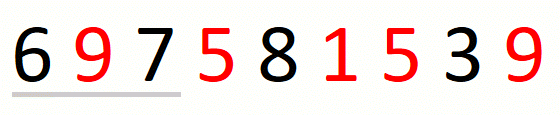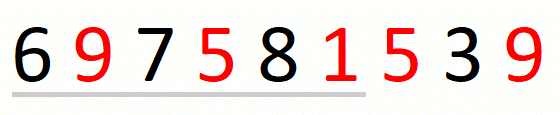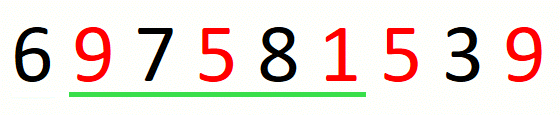
Finding the leftmost candidate consists in expanding the window to the
right until we cover all characters in the input set. When we do not
find all characters in the set, we know that there is no solution and
we return the empty string. For string 697581539 and set {1,5,9},
the process is the following.
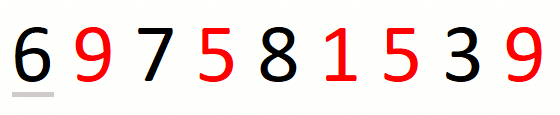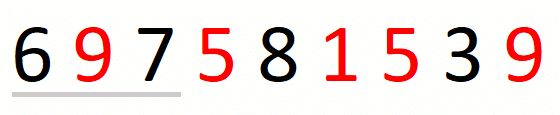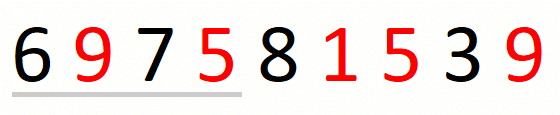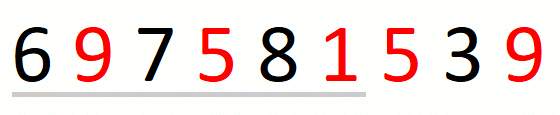
Refining the leftmost pre-candidate into the leftmost candidate
consists in contracting the window to the right until we cannot drop a
character. We cannot drop a character when the character is in the
input set and there are no more copies of the character in the window.
For string 697581539 and set {1,5,9}, the process is the
following.

We transform a candidate solution into the next by a sequence of expansions and contractions of the window. Every expansion extends the window by one position. A given expansion is not followed by a contraction when we cannot drop the first character in the window. A given contraction drops characters until we cannot do it anymore. This part of the approach is the following.
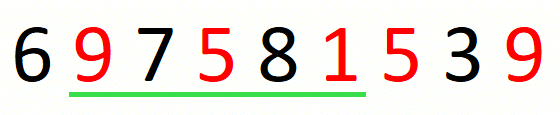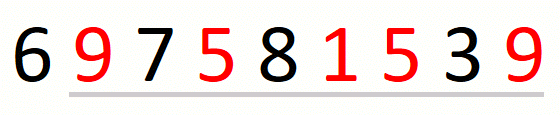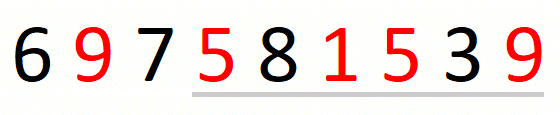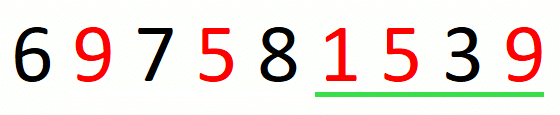
We update the current solution after every contraction of the window.
Implementation
The following is our Ruby implementation of the approach.
1: #!/usr/bin/env ruby
2:
3: def get_initial_right c, s
4: found = 0
5: r = 0
6: while found < c.length && r < s.length
7: if c.has_key? s[r]
8: c[s[r]] += 1
9: if c[s[r]] == 1
10: found += 1
11: end
12: end
13: r += 1
14: end
15: return -1 if found < c.length
16: return r - 1
17: end
18:
19: def shortest_substring_that_contains_letters s, allowed
20:
21: return s if allowed == []
22:
23: c = {}
24: allowed.chars.each { |n| c[n] = 0 }
25: l = 0
26: r = get_initial_right c, s
27:
28: return '' if r == -1
29:
30: min_len = r - l + 1
31: min_l = l
32: min_r = r
33:
34: while true
35:
36: # contract window
37: while true
38: if c.has_key? s[l]
39: if c[s[l]] == 1
40: break
41: else
42: c[s[l]] -= 1
43: end
44: end
45: l += 1
46: end
47:
48: # update best solution
49: len = r - l + 1
50: if len < min_len
51: min_len = len
52: min_l = l
53: min_r = r
54: end
55:
56: # expand window
57: r += 1
58: break if r == s.length
59: if c.has_key? s[r]
60: c[s[r]] += 1
61: end
62:
63: end
64:
65: return s[min_l..min_r]
66:
67: end
68:
69: while true
70: a = readline.strip rescue break
71: b = readline.strip rescue break
72: puts shortest_substring_that_contains_letters a, b
73: endProcedure get_initial_right corresponds to finding the first
pre-candidate. The main loop of
shortest_substring_that_contains_letters corresponds to the rest of
the approach. Variables l and r indicate the boundaries of the
window.
The crucial aspect of the implementation is counting characters
covered by the window. We use dictionary c for that purpose.
Dictionary c consists of a counter for each character in the input
set.
We use dictionary c in the following way. Procedure
get_initial_right counts the characters for the first pre-candidate.
When we contract, we use c to never drop a character that we cannot
drop. When we contract and we reach a character in the input set, we
stop when this is the only copy left in the window (line 39) and we
decrease its counter when there is at least another copy (line 42).
When we expand and we reach a character in the input set, we increase
the counter of the character.
The main loop stops when we cannot expand the window anymore (line 58).
The runtime of our implementation is $@O(n)@$ where $@n@$ is the length of the input string. The reason is that the number of iterations of nested loop (lines 37 to 46) is bounded by the length of the input string.