Alternative Approach: All Balanced Parentheses Strings
We explain another approach to solving All Balanced Parentheses Strings and implement the approach in Ruby and Golang.
If you haven’t read All Balanced Parentheses Strings, do it now.
Solution
The structure of any given string consisting of n balanced pairs of
parentheses falls in one of the following two cases.
Case n = 0. The empty string is the only balanced
parentheses string that has no pair of parentheses.
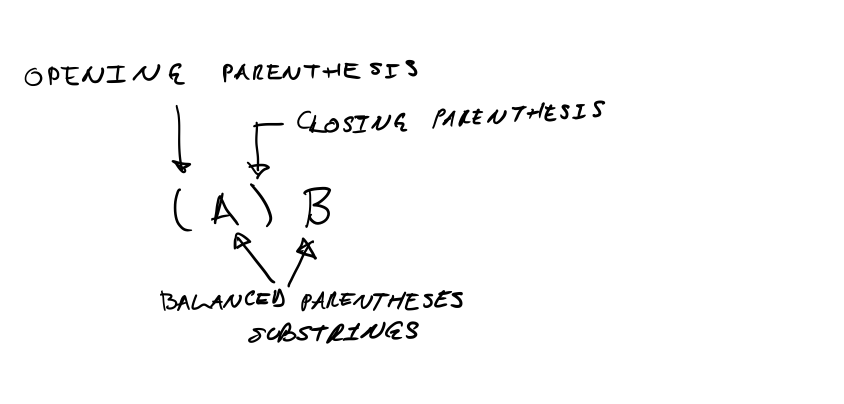
Case n > 0. The following diagram illustrates the structure of the
given string.
For example, consider string (()()).
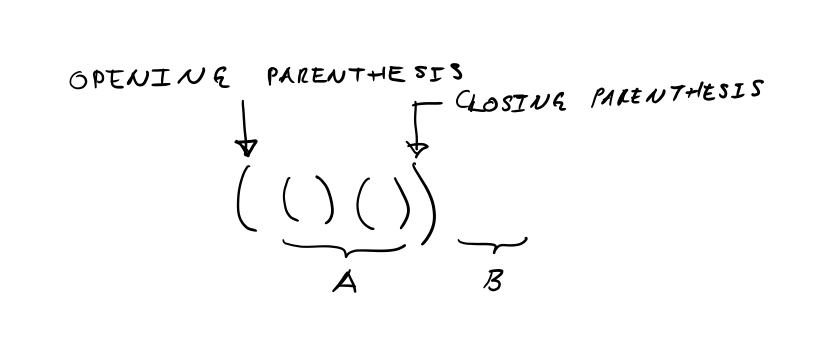
The string begins with an opening parenthesis and contains a
corresponding closing parenthesis. The example contains substring
()() between the opening and closing parentheses, which corresponds
to A in the previous diagram. The example does not have a substring
after the closing parenthesis, so the empty string corresponds to B
in the previous diagram.
As another example, consider string ()(()).
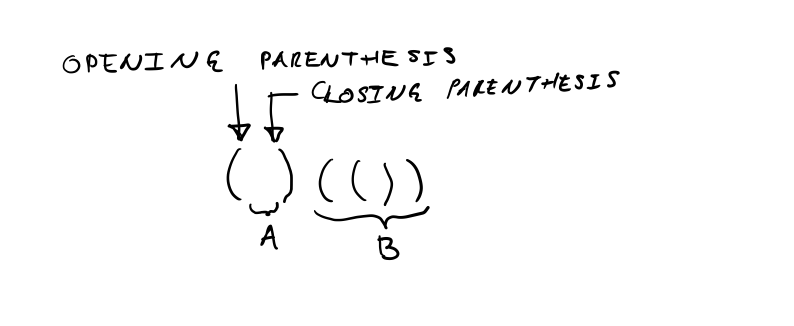
In this example, the empty string corresponds to A in the previous
diagram and substring (()) corresponds to B.
Each example satisfies the condition that the sum of balanced pairs
of parentheses in A and B is one less than the count of balanced
pairs of parentheses in the whole string.
Our approach to enumerating all strings for a given n consists in
recursively applying the two cases to the construction of all pairs of
substrings A and B that satisfy condition
pairs(A) + pairs(B) = n - 1.
For example, for the construction of all strings where n = 3, we
construct the strings for n = 2, 1, 0, and concatenate all pairs
that satisfy the condition with opening and closing parentheses, like
so.
** n = 0 **
Strings with 0 pairs
---------------------------------
The empty string
** n = 1 **
pairs(A) | pairs(B) | A | B | Strings with 1 pair
----------|----------|------|------|----------------------
0 | 0 | | | ()
** n = 2 **
pairs(A) | pairs(B) | A | B | Strings with 2 pairs
----------|----------|------|------|----------------------
0 | 1 | | () | ()()
1 | 0 | () | | (())
** n = 3 **
pairs(A) | pairs(B) | A | B | Strings with 3 pairs
----------|----------|------|------|----------------------
0 | 2 | | ()() | ()()()
0 | 2 | | (()) | ()(())
1 | 1 | () | () | (())()
2 | 0 | ()() | | (()())
2 | 0 | (()) | | ((()))Our application of the two cases corresponds to the application of the
following recursive definition of the set $@e_n@$ of strings
consisting of n balanced pairs of parentheses.
$@ e_0 = \{ “” \} @$
$@ e_n = \{ “\text{(}A\text{)}B” \mid \exists i, j : A \in e_i \wedge B \in e_j \wedge i + j = n - 1 \} @$
Implementation
We implement the solution in Ruby and Golang.
Our Ruby implementation is the following.
#!/usr/bin/env ruby
$e = Hash.new
def e n
if n == 0
return ['']
elsif $e.has_key? n
return $e[n]
end
$e[n] = []
i = 0
j = n - 1
while i < n
e(i).each do |a|
e(j).each do |b|
$e[n] << "(#{a})#{b}"
end
end
i += 1
j -= 1
end
return $e[n]
end
while true
n = readline.strip.to_i rescue break
puts e n
endOur Golang implementation is the following.
package main
import (
"bufio"
"os"
"fmt"
"strconv"
)
var e_ map[int][]string
func e(n int) ([]string) {
if n == 0 {
return []string{""}
} else if _, exists := e_[n]; exists {
return e_[n]
}
e_[n] = make([]string, 0, 1)
i := 0
j := n - 1
for i < n {
for _, a := range e(i) {
for _, b := range e(j) {
e_[n] = append(e_[n], "(" + a + ")" + b)
}
}
i += 1
j -= 1
}
return e_[n]
}
func main() {
e_ = make(map[int][]string)
scanner := bufio.NewScanner(os.Stdin)
for scanner.Scan() {
n, err := strconv.Atoi(scanner.Text())
if err != nil { break }
for _, s := range e(n) {
fmt.Printf("%s\n", s)
}
}
}